Для построения гистограммы надо рассчитать относительные частоты. Объем выборки: n=5+8+16+12+9=50. Длина интервалов: h=2. Относительные частоты определяются по формуле: 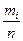 . Их значения равны для соответствующих интервалов: 0.1; 0.16; 0.32; 0.24; 0.18. Интервальный вариационный ряд графически изображают с помощью гистограммы. Для ее построения на оси х откладывают отрезки частичных интервалов варьирования, на них строят прямоугольники высотой, равной относительной частоте. Для заданного примера гистограмма приведена на Рис. 12.
. Их значения равны для соответствующих интервалов: 0.1; 0.16; 0.32; 0.24; 0.18. Интервальный вариационный ряд графически изображают с помощью гистограммы. Для ее построения на оси х откладывают отрезки частичных интервалов варьирования, на них строят прямоугольники высотой, равной относительной частоте. Для заданного примера гистограмма приведена на Рис. 12.
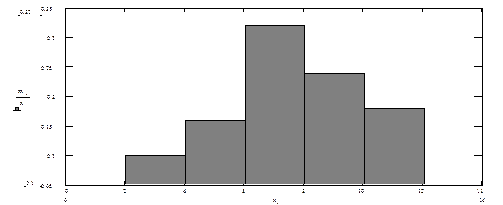
Рис.12
5. Из нормальной генеральнойсовокупности с параметрами 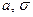 с известным средним квадратическим отклонением
с известным средним квадратическим отклонением 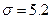 извлечена выборка объема
извлечена выборка объема 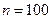 и по ней найдена выборочная средняя
и по ней найдена выборочная средняя 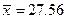 . Требуется при уровне значимости
. Требуется при уровне значимости 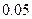 по сгруппированным данным проверить нулевую гипотезу
по сгруппированным данным проверить нулевую гипотезу 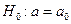
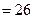 при конкурирующей гипотезе
при конкурирующей гипотезе 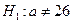 .
.
Решение. Данная задача относится к задачам проверки статистических гипотез, а именно, производитсясравнение выборочной средней с гипотетической генеральной средней для нормальной совокупности, если дисперсия генеральной совокупности известна.
Для того, чтобы при заданном уровне значимости 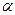 проверить нулевую гипотезу
проверить нулевую гипотезу 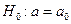 о равенстве генеральной средней
о равенстве генеральной средней 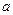 нормальной совокупности с известной дисперсией
нормальной совокупности с известной дисперсией 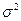 гипотетическому (предполагаемому) значению
гипотетическому (предполагаемому) значению 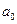 , при конкурирующей гипотезе
, при конкурирующей гипотезе 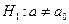 , надо:
, надо:
- вычислить наблюдаемое значение критерия 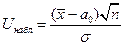 ,
,
- по таблице значений функции Лапласа найти критическую точку 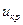 двусторонней критической области из равенства
двусторонней критической области из равенства 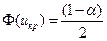 .
.
Если 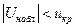 - нулевую гипотезу принимают, если
- нулевую гипотезу принимают, если 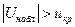 - нулевую гипотезу отвергают. Найдем наблюдаемое значение критерия:
- нулевую гипотезу отвергают. Найдем наблюдаемое значение критерия:
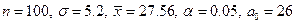 ;
; 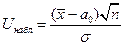
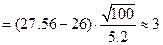 .
.
По условию, конкурирующая гипотеза имеет вид 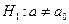 , поэтому критическая область – двусторонняя.
, поэтому критическая область – двусторонняя.
Найдем критическую точку из равенства 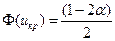
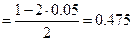 . По таблице функции Лапласа находим
. По таблице функции Лапласа находим 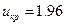 . Так как
. Так как 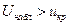 - нулевую гипотезу отвергаем, т.е выборочная и гипотетическая средние различаются значимо.
- нулевую гипотезу отвергаем, т.е выборочная и гипотетическая средние различаются значимо.
Ответ. Гипотеза о том, что параметр 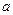 нормальной генеральной совокупности равен 26, отвергается, т.к. не соответствует выборочным данным.
нормальной генеральной совокупности равен 26, отвергается, т.к. не соответствует выборочным данным.
5. Найти выборочное уравнение линейной регрессии  на
на  по данным корреляционной таблицы.
по данным корреляционной таблицы.
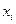 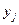 | ||||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - |
Решение. В том случае, когда варианты парной выборки встречаются по нескольку раз, причем с одним значением варианты 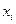 может встретиться несколько вариант
может встретиться несколько вариант 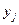 , их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечают частоту
, их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечают частоту 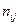 выбора соответствующей пары (
выбора соответствующей пары (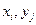 ). Частоты вариант находят как суммы по строкам и столбцам:
). Частоты вариант находят как суммы по строкам и столбцам: 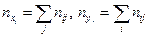 . Очевидно, что
. Очевидно, что 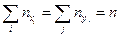 - объем выборки.
- объем выборки.
Выборочное уравнение прямой линии регрессии  на
на  имеет вид
имеет вид 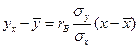 ,
,
где 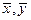 - выборочные средние для случайных величин
- выборочные средние для случайных величин  и
и  ;
; 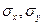 - выборочные средние квадратические отклонения;
- выборочные средние квадратические отклонения; 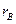 - выборочный коэффициент корреляции, причем
- выборочный коэффициент корреляции, причем 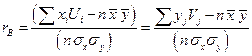 ,
, 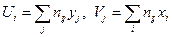 .
.
Выборочное уравнение прямой линии регрессии  на
на  имеет вид
имеет вид 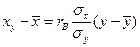 .
.
Если данные наблюдений над признаками  и
и  заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:
заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам: 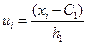 ,
, 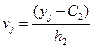 , где
, где 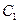 - «ложный нуль» вариант
- «ложный нуль» вариант  (новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту);
(новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту); 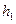 - шаг, т.е. разность между двумя соседними вариантами
- шаг, т.е. разность между двумя соседними вариантами  ;
; 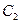 - ложный путь вариант
- ложный путь вариант  ;
; 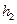 - шаг вариант
- шаг вариант  .
.
В этом случае выборочный коэффициент корреляции 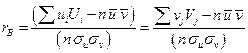 ,
, 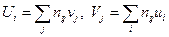 .
.
Величины 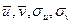 могут быть найдены по формулам:
могут быть найдены по формулам: 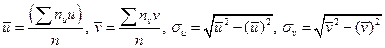 .
.
По этим значениям можно определить входящие в уравнения регрессии величины по формулам: 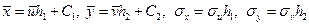 .
.
В заданной корелляционной таблице выберем в качестве ложных нулей 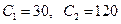 . Шаг варианты
. Шаг варианты 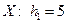 , шаг варианты
, шаг варианты 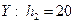 . Для упрощения расчетов введем условные варианты
. Для упрощения расчетов введем условные варианты 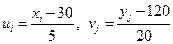 и составим преобразованную корреляционную таблицу с условными вариантами, в которую внесем значения
и составим преобразованную корреляционную таблицу с условными вариантами, в которую внесем значения 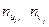 :
:
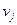 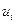 | -3 | -2 | -1 | 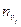 | |||
| -1 | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | - | ||||||
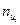 | 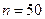 |
Затем составим новую таблицу, в которую внесем найденные значения 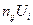 в правый верхний угол заполненной клетки и
в правый верхний угол заполненной клетки и 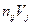 в левый нижний угол, по центру остается частота. После этого суммируем верхние значения по строкам для получения значений
в левый нижний угол, по центру остается частота. После этого суммируем верхние значения по строкам для получения значений 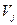 и нижние значения по столбцам для
и нижние значения по столбцам для 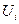 и подсчитаем величины
и подсчитаем величины 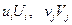 :
:
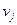 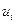 | -3 | -2 | -1 | 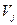 | 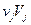 | |||
| -1 | -6 -2 | -2 -1 | - | -7 | - | - | -8 | |
| -12 | - | -2 | - | - | -8 | |||
| - | -10 | - | -1 | -1 | ||||
| - | - | -3 | ||||||
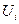 | -2 | - | 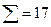 | |||||
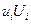 | -8 | -6 | 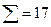 | - |
Проверяем суммы 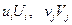 , получаем
, получаем 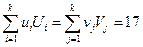 .
.
Находим 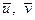 (умножаем значение варианты на сумму ее частот и находим среднее арифметическое этих величин):
(умножаем значение варианты на сумму ее частот и находим среднее арифметическое этих величин):
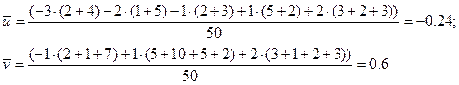
Находим 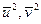 :
:
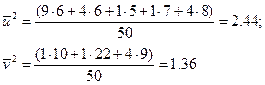
Определяем 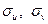 :
:
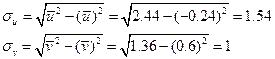
Вычисляем выборочный коэффициент корреляции 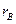 :
:
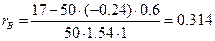
Осуществим переход к исходным вариантам:
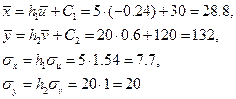
Находим уравнение линии регрессии  на
на  :
: 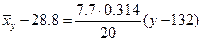 или
или 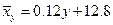 . Аналогично, уравнение линии регрессии
. Аналогично, уравнение линии регрессии  на
на  :
:
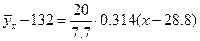 или
или 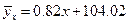 .
.
Ответ. Линии регрессии имеют вид: 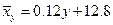 и
и 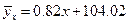 .
.
Варианты заданий контрольной работы № 8
Таблица 6. Варианты задания 1
| № варианта | Задача. |
| В урне 20 шаров с номерами № 1, № 2, № 3, …,№ 20. Какова вероятность вынуть шар с № 37? | |
Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 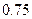 , вторым стрелком - , вторым стрелком - 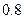 , третьим - , третьим - 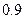 . Определить вероятность того, что все три стрелка одновременно попадут в цель. . Определить вероятность того, что все три стрелка одновременно попадут в цель. | |
| В ящике 10 деталей, из которых 4 – окрашены. Наудачу взяли 3 детали. Найти вероятность того, что хотя бы одна из них окрашена. | |
| Брошено 6 игральных костей. Найти вероятность события, заключающегося в том, что на всех костях окажется разное количество очков. | |
Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 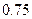 , вторым стрелком - , вторым стрелком - 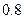 , третьим - , третьим - 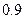 . Определить вероятность того, что в цель попадает хотя бы один стрелок. . Определить вероятность того, что в цель попадает хотя бы один стрелок. | |
| Эксперимент состоит в подбрасывании двух костей. Найти вероятность того, что выпадет дубль. | |
| В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 5 черных шаров. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые? | |
| В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 5 черных шаров. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой черный. | |
| Имеются три одинаковых ящика. В первом ящике 20 белых шаров. Во втором ящике 10 белых и 10 черных шаров. Из выбранного наугад ящика вынули белый шар. Найти вероятность того, что шар вынут из первого ящика. | |
| В ящике имеется N изделий, среди которых могут быть и бракованные. Вынутое наугад изделие оказалось набракованным. Определить вероятность того, что: а) все изделия в ящике небракованные; б) N-1 изделий небракованных и одно изделие бракованное (в предположении равновозможности любого состава изделий). | |
| В ящике 6 белых и 8 черных шаров. Из ящика вынули 2 шара (не возвращая вынутый шар в ящик). Найти вероятность того, что оба шара белые. | |
| В ящике а белых и б черных шаров. Какова вероятность того, что из двух вынутых шаров один белый, а другой черный? (Вынутый шар в урну не возвращается.) | |
| В первом ящике 6 шаров: 1 белый, 2 красных и 3 синих. Во втором ящике 12 шаров: 2 белых, 6 красных и 4 синих. Из каждого ящика вынули по шару. Найти вероятность того, что среди вынутых шаров нет синих? | |
Вероятность того, что в течение дня произойдет неполадка станка, равна 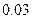 . Какова вероятность того, что в течение 4 дней подряд не произойдет ни одной неполадки? . Какова вероятность того, что в течение 4 дней подряд не произойдет ни одной неполадки? | |
Однотипные приборы изготавливаются 3 заводами в количественном отношении: 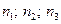 . Причем вероятности брака для этих заводов: . Причем вероятности брака для этих заводов: 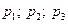 . Приобретенный прибор оказывается бракованным. Какова вероятность того, что прибор выпущен первым заводом. . Приобретенный прибор оказывается бракованным. Какова вероятность того, что прибор выпущен первым заводом. | |
Число грузовых машин, проезжающих по шоссе на котором стоит бензоколонка, относится к числу проезжающих легковых машин как 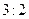 . Вероятность того, что грузовая машина будет заправляться равна . Вероятность того, что грузовая машина будет заправляться равна 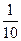 , легковая - , легковая - 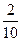 . Какова вероятность того, что проезжающая машина приедет на заправку. . Какова вероятность того, что проезжающая машина приедет на заправку. | |
Для сигнализации об аварии установлены 2 независимо работающих датчика. Вероятность того, что при аварии сработает: первый датчик 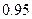 , для второго - , для второго - 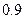 . Найти вероятность того, что при аварии сработает только один датчик. . Найти вероятность того, что при аварии сработает только один датчик. | |
| В урне 9 белых и 1 черный шар. Вынули сразу 3 шара. Какова вероятность того, что все шары белые? | |
| В колоде 52 карты, вытаскивают одну карту. Найти вероятность того, что: а) вынули туз, б) вынули карту черной масти. | |
При одном цикле обзора объект обнаруживается с вероятностью 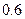 . Какова вероятность, что объект будет обнаружен при 3-х циклах обзора. При каждом цикле объект обнаруживается независимо. . Какова вероятность, что объект будет обнаружен при 3-х циклах обзора. При каждом цикле объект обнаруживается независимо. | |
Между двумя игроками проводится 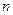 партий, причем каждая партия заканчивается выигрышем или проигрышем. Все возможные исходы равновероятны. Какова вероятность того, что определенный игрок выиграет партий, причем каждая партия заканчивается выигрышем или проигрышем. Все возможные исходы равновероятны. Какова вероятность того, что определенный игрок выиграет  партий. партий. | |
Производится 3 выстрела по одной мишени. Вероятность попадания при каждом выстреле равна 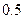 . Найти вероятность того, что в результате этих выстрелов будет только одно попадание . Найти вероятность того, что в результате этих выстрелов будет только одно попадание | |
В зале насчитывается 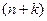 мест, случайным образом занимают места мест, случайным образом занимают места 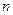 человек. Определить вероятность того, что будут заняты определенные человек. Определить вероятность того, что будут заняты определенные  мест ( мест (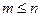 ). ). | |
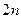 футбольных команд разбиваются на 2 подгруппы. Определить вероятность того, что 2 наиболее сильные команды, окажутся: а) в разных подгруппах; б) в одной подгруппе. футбольных команд разбиваются на 2 подгруппы. Определить вероятность того, что 2 наиболее сильные команды, окажутся: а) в разных подгруппах; б) в одной подгруппе. | |
| В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны: а)два мальчика; б)девочка и мальчик? |
Таблица 7. Варианты задания 2
| № варианта | Задача. |
Вероятность появления события А равна 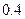 . Какова вероятность того, что при 10 испытаниях событие А появится не больше трех раз? . Какова вероятность того, что при 10 испытаниях событие А появится не больше трех раз? | |
| Определить вероятность того, что в семье, имеющей 5 детей, будет 3 девочки и 2 мальчика. Вероятности рождения мальчика и девочки считать одинаковыми. | |
| Две игральные кости подбрасываются 7 раз. Найти вероятности событий: а) сумма очков равная 7 выпадет дважды. б) сумма очков равная 7 выпадет по крайне мере 1 раз. | |
| Две игральные кости подбрасываются 7 раз. Найти вероятности событий: а) ни разу не выпадет сумма равная 12 очкам; б) каждый раз выпадет сумма больше 7; | |
| Монету подбрасывают 5 раз. Какова вероятность, что герб выпал 3 раза. | |
Вероятность того, что стрелок попадет в десятку равна 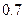 , в девятку - , в девятку - 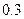 . Определить вероятность того, что данный стрелок при 3-х выстрелах наберет 29 очков. . Определить вероятность того, что данный стрелок при 3-х выстрелах наберет 29 очков. | |
Станок – автомат штампует детали. Вероятность того, что за смену не будет выпущено ни одной нестандартной детали 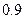 . Определить вероятность того, что за 3 смены не будет выпущено ни одной нестандартной детали. . Определить вероятность того, что за 3 смены не будет выпущено ни одной нестандартной детали. | |
Вероятность того, что при одном измерении некоторой величины будет допущена ошибка, превышающая заданную точность равна 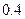 . Произведено 3 независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. . Произведено 3 независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. | |
Стрелок с вероятностью 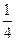 попадает в яблочко. Произведено 5 выстрелов. Найти вероятности событий: а) хотя бы одно попадание в яблочко; б) ровно одно попадание в яблочко. попадает в яблочко. Произведено 5 выстрелов. Найти вероятности событий: а) хотя бы одно попадание в яблочко; б) ровно одно попадание в яблочко. | |
Производится стрельба по цели тремя снарядами. Снаряды попадают в цель независимо друг от друга. Для каждого снаряда вероятность попадания равна 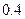 . Если в цель попал первый снаряд, он поражает цель с вероятностью . Если в цель попал первый снаряд, он поражает цель с вероятностью 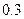 , если второй - , если второй - 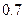 , если третий - , если третий - 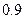 . Найти вероятность поражения цели. . Найти вероятность поражения цели. | |
| Два противника играют в шахматы только до победы (вероятность выигрыша у каждого равна 0.5). Что вероятнее: выиграть одну из двух, две из четырех. | |
| Определить вероятность того, что в семье, имеющей 5 детей, будет не больше 3-х девочек (вероятность рождения девочки 0.55). | |
| Монета подбрасывается 6 раз. Какова вероятность того, что 6 раз она упадет гербом вверх? | |
| Монета подбрасывается 6 раз. Какова вероятность того, что она упадет гербом вверх не больше 3-х раз? | |
| В классе 30 учеников: 20 мальчиков и 10 девочек. На каждый из трех вопросов, заданных учителем, ответили по одному ученику. Какова вероятность того, что среди ответивших было два мальчика и одна девочка? | |
| В каждом из 4-х ящиков по 5 белых и по 15 черных шаров. Из каждого ящика вынули по одному шару. Какова вероятность вынуть два белых и два черных шара? | |
Вероятность появления события 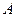 равна равна 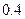 . Какова вероятность того, что событие . Какова вероятность того, что событие 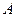 появится не больше трех раз в пяти испытаниях? появится не больше трех раз в пяти испытаниях? | |
Вероятность попадания стрелком в десятку равна 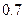 , в девятку - , в девятку - 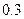 . Определить вероятность того, что данный стрелок при 3-х выстрелах наберет 29 очков. . Определить вероятность того, что данный стрелок при 3-х выстрелах наберет 29 очков. | |
| Две игральные кости подбрасываются 7 раз. Найти вероятности событий: а)ни разу не выпадет сумма равная 12 очкам; б) каждый раз выпадет сумма больше 7; | |
| Брошено 6 игральных костей. Найти вероятность события, заключающегося в том, что на всех костях окажется разное количество очков. | |
| Монета подбрасывается 6 раз. Какова вероятность того, что 6 раз она упадет гербом вверх? | |
Вероятность появления события А равна 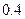 . Какова вероятность того, что при 10 испытаниях событие А появится не больше трех раз? . Какова вероятность того, что при 10 испытаниях событие А появится не больше трех раз? | |
| Два противника играют в шахматы только до победы (вероятность выигрыша у каждого равна 0.5). Что вероятнее: выиграть одну из двух или две из четырех. | |
| Два противника играют в шахматы только до победы (вероятность выигрыша у каждого равна 0.5). Два равносильных противника играют в шахматы. Что вероятнее: выиграть не менее 2 из 4 партий или не менее 3-х из 5? | |
Стрелок с вероятностью 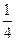 попадает в яблочко. Произведено 5 выстрелов. Найти вероятности событий: а) ровно 2 попадания в яблочко; б) не менее 3-х попаданий в яблочко. попадает в яблочко. Произведено 5 выстрелов. Найти вероятности событий: а) ровно 2 попадания в яблочко; б) не менее 3-х попаданий в яблочко. |
Таблица 8. Варианты задания 3
| № варианта | Задача. |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 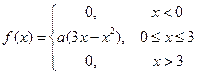 . Найти: а) коэффициент а, б) вероятность попадания X в промежуток . Найти: а) коэффициент а, б) вероятность попадания X в промежуток 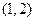 . . | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 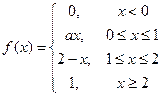 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 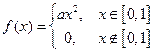 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 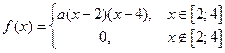 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 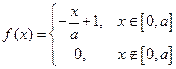 . Найти: а) коэффициент а, б)математическое ожидание и дисперсию. . Найти: а) коэффициент а, б)математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 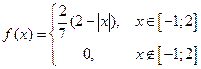 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X задана функцией распределения 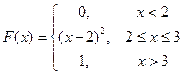 . Найти плотность распределения и дисперсию случайной величины. . Найти плотность распределения и дисперсию случайной величины. | |
Дана плотность распределения случайной величины Х: 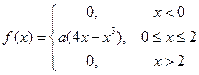 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Дана плотность распределения случайной величины X: 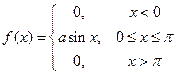 . Найти: а) коэффициент а, б) функцию распределения . Найти: а) коэффициент а, б) функцию распределения 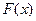 . . | |
Дана функция распределения: 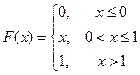 . Найти: математическое ожидание и дисперсию. . Найти: математическое ожидание и дисперсию. | |
Случайная величина X задана функцией распределения 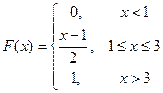 . Вычислить вероятность попадания случайной величины X винтервалы: а) (1.5; 2.5), б (2.5; 3.5). . Вычислить вероятность попадания случайной величины X винтервалы: а) (1.5; 2.5), б (2.5; 3.5). | |
Случайная величина X характеризуется рядом распределения 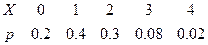 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 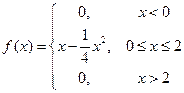 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 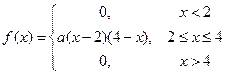 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 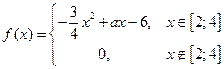 . Найти: а) коэффициент а, б) функцию распределения . Найти: а) коэффициент а, б) функцию распределения 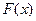 . . | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 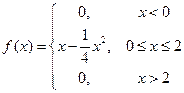 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. | |
Случайная величина X характеризуется рядом распределения 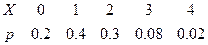 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. | |
Дана функция распределения: 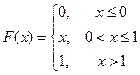 . Найти: математическое ожидание и дисперсию. . Найти: математическое ожидание и дисперсию. | |
Дана плотность распределения случайной величины X: 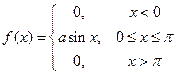 . Найти: а) коэффициент а, б) функцию распределения . Найти: а) коэффициент а, б) функцию распределения 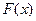 . . | |
Случайная величина X задана функцией распределения 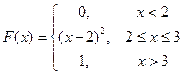 . Найти плотность распределения и дисперсию. . Найти плотность распределения и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 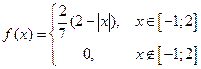 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 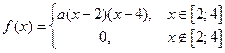 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 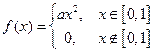 . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. . Найти: а) коэффициент а, б) математическое ожидание и дисперсию. | |
Случайная величина X подчинена закону распределения с плотностью  , причем , причем 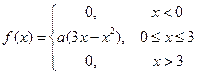 . Найти: а) коэффициент а, б) вероятность попадания X в промежуток . Найти: а) коэффициент а, б) вероятность попадания X в промежуток 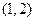 . . | |
Дана функция 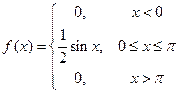 . Найти математическое ожидание и дисперсию. . Найти математическое ожидание и дисперсию. |
Таблица 9. Варианты задания 4
| Вариант | 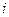 | 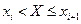 | 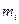 | Вариант | 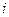 | 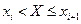 | 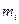 |
| 2-4 | 2-5 | ||||||
| 4-6 | 5-8 | ||||||
| 6-8 | 8-11 | ||||||
| 8-10 | 11-14 | ||||||
| 10-12 | 14-17 | ||||||
| 3-7 | 10-14 | ||||||
| 7-11 | 14-18 | ||||||
| 11-15 | 18-22 | ||||||
| 15-19 | 22-26 | ||||||
| 19-23 | 26-30 | ||||||
| 10-12 | 5-10 | ||||||
| 12-14 | 10-15 | ||||||
| 14-16 | 15-20 | ||||||
| 16-18 | 20-25 | ||||||
| 18-20 | 25-30 | ||||||
| 3-7 | 10-20 | ||||||
| 7-11 | 20-30 | ||||||
| 11-15 | 30-40 | ||||||
| 15-19 | 40-50 | ||||||
| 19-23 | 50-60 | ||||||
| 4-8 | 15-30 | ||||||
| 8-12 | 30-45 | ||||||
| 12-16 | 45-0 | ||||||
| 16-20 | 60-75 | ||||||
| 20-24 | 75-90 | ||||||
| 7-9 | 20-40 | ||||||
| 9-11 | 40-60 | ||||||
| 11-13 | 60-80 | ||||||
| 13-15 | 80-100 | ||||||
| 15-17 | 100-120 | ||||||
| 5-8 | 2-6 | ||||||
| 8-11 | 6-10 | ||||||
| 11-14 | 10-14 | ||||||
| 14-17 | 14-18 | ||||||
| 17-20 | 18-22 | ||||||
| 4-6 | 14-16 | ||||||
| 6-8 | 16-18 | ||||||
| 8-10 | 18-20 | ||||||
| 10-12 | 20-22 | ||||||
| 12-14 | 22-24 | ||||||
| 1-5 | 5-10 | ||||||
| 5-9 | 10-15 | ||||||
| 9-13 | 15-20 | ||||||
| 13-17 | 20-25 | ||||||
| 17-21 | 25-30 | ||||||
| 10-14 | 3-5 | ||||||
| 14-18 | 5-7 | ||||||
| 18-22 | 7-9 | ||||||
| 22-26 | 9-11 | ||||||
| 26-30 | 11-13 | ||||||
| 20-22 | 4-9 | ||||||
| 22-24 | 9-14 | ||||||
| 24-26 | 14-19 | ||||||
| 26-28 | 19-24 | ||||||
| 28-30 | 24-29 | ||||||
| 5-7 | 4-10 | ||||||
| 7-9 | 10-16 | ||||||
| 9-11 | 16-22 | ||||||
| 11-13 | 22-28 | ||||||
| 13-15 | 28-34 | ||||||
| 11-14 | |||||||
| 14-17 | |||||||
| 17-20 | |||||||
| 20-23 | |||||||
| 23-26 |
Таблица 10. Варианты задания 5
| Вариант | 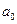 | 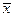 | 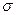 | Вариант | 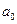 | 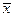 | 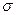 |
Таблица 11. Варианты задания 6
| Вариант | Корреляционная таблица | Вариант | Корреляционная таблица | |||||||||||||
  |   | |||||||||||||||
  |   | |||||||||||||||
  |   | |||||||||||||||
  |   | |||||||||||||||
  |   | |||||||||||||||
  |   | |||||||||||||||
|
 Сейчас читают про:
|
 2015-04-01
2015-04-01 1171
1171






