Уравнение прямой в пространстве, проходящей через две точки.
M1(x1;y1;z1) M2(x2;y2;z2)
В качестве направляющего вектора можно задать вектор 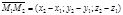
Следовательно:
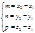 , тогда
, тогда 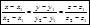
Две прямые в пространстве могут пересекаться, быть параллельными и скрещиваться. Если две прямые пересекаются или параллельны, то они лежат в одной плоскости. Пусть две прямые заданы каноническими уравнениями:
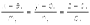 и
и 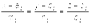
где 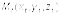 и
и 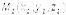 - точки принадлежащие прямым. Очевидно, чтобы прямые лежали в одной плоскости необходимо и достаточно чтобы векторы
- точки принадлежащие прямым. Очевидно, чтобы прямые лежали в одной плоскости необходимо и достаточно чтобы векторы 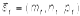 ,
, 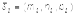 и
и 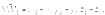 были компланарны, то есть их смешанное произведение равно нулю:
были компланарны, то есть их смешанное произведение равно нулю:
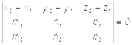 - условие принадлежности двух прямых одной плоскости.
- условие принадлежности двух прямых одной плоскости.
Угол между прямыми.
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами 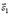 и
и 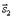 . Так как
. Так как 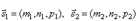 , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим
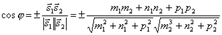 .
.
 2015-05-30
2015-05-30 239
239








