2015-05-30
213
Канонические уравнения прямой.
S(m;n;p) – направляющий вектор прямой L. M0(x0;y0;z0) – точка на прямой.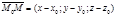 
соединяет M0 с произвольной точкой М.
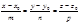
Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
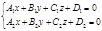
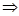
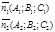
Т.к. прямая перпендикулярна векторам n1 и n2 то направляющий вектор запишется как векторное произведение:
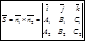
Переход от общих уравнений к каноническим.
Если придать одной переменной из системы, кот указана выше, пост знач-е, то можно перейти от общего ур, к канон.
Эллиптический параболоид.
Поверхности 2-го порядка. Параболоиды.
Эллиптический. При пересечении поверхности координатами плоскостями Oxz и Oyz получается соответственно параболы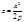 
и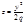 
. Таким образом, поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно расширяющейся чаши.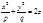 
6 БИЛЕТ:
