Измерение геометрических параметров дороги выполняют с целью выявления влияния дорожных условий на аварийность и, в случае разбора конкретного ДТП, на механизм происшествия. В последнем случае устанавливают в процессе судебно-автодорожной экспертизы конкретные значения вероятностей возникновения данного ДТП под влиянием:
– дорожных условий (rду) и причин их ухудшающих (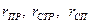 ) по формулам (1.79), (1.81) и (1.83);
) по формулам (1.79), (1.81) и (1.83);
– уровня содержания дороги под воздействием погодных факторов (rсд) по формуле (1.76);
– действий (или бездействия) водителя (rв) или действий пешехода (rп) по формулам (1.72), (1.73), (1.74), (1.75), (1.77), (1.78), (1.80) и (1.84).
Причем измеряют только те геометрические параметры дороги, которые могли способствовать развитию аварийной ситуации. Используя эти вероятности (rду, rсд, rпр, rстр, rсп , rв, rп), следствие и судебные органы могут ставить вопрос об индивидуальной ответственности участников происшествия (материальной, административной или уголовной) и выносить частные определения в адрес проектной, строительной и дорожно-эксплуатационной организаций, а также органов ГИБДД, включая требования по разработке мер, предупреждающих ДТП, или по улучшению дорожных условий на данном участке дороги, если его параметры или состояние способствуют высокой аварийности [,, ].
Вычислить перечисленные вероятности можно только в том случае, когда в процессе осмотра геометрических параметров получают достаточное для статистических расчётов число измерений в пределах одного элемента (в пределах: кривой в плане, выпуклой или вогнутой кривой, ширины покрытия и т.д.).
Измерение геометрических параметров выполняют с помощью ходовой дорожной лаборатории на базе микроавтобуса [5] или при её отсутствии методами описанными ниже.
4.2.1. Определение радиусов кривых в плане
Необходимое для статистических расчётов число радиусов в пределах круговой кривой получают в результате натурных измерений хорды произвольной длины 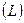 и ординат
и ординат 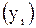 , расположенных через равные отрезки
, расположенных через равные отрезки 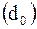 между хордой и кромкой покрытия (рис.2.5). Основным условием измерений является следующее: среди измеренных ординат должна присутствовать ордината, откладываемая от середины хорды
между хордой и кромкой покрытия (рис.2.5). Основным условием измерений является следующее: среди измеренных ординат должна присутствовать ордината, откладываемая от середины хорды 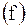 . Это условие выполняют путём деления измеренной хорды
. Это условие выполняют путём деления измеренной хорды 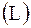 пополам и разбивки обеих половин хорды
пополам и разбивки обеих половин хорды 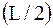 на одинаковое число интервалов
на одинаковое число интервалов 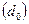 .
.
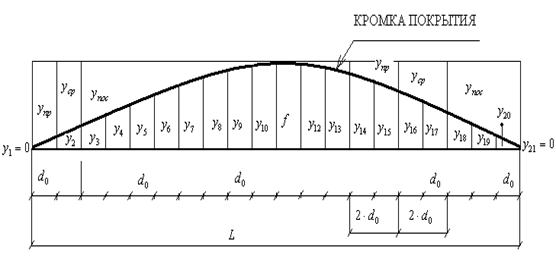
Рис.2.5. К определению радиусов кривой в плане по трём ординатам:
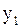 ,
, 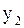 ,…,
,…, 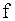 ,…,
,…, 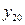 ,
, 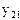 – измеренные ординаты кривой;
– измеренные ординаты кривой;
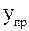 ,
, 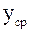 ,
, 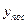 – примеры вычисляемых ординат по трём измерениям (через интервалы
– примеры вычисляемых ординат по трём измерениям (через интервалы 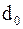 и
и 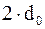 ).
).
Величины радиусов круговой кривой определяют по формуле [6]:
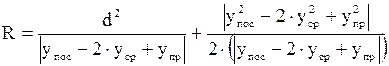 , ,
| (2.1) |
где
d – отрезки постоянной длины на хорде, стягивающей дугу закругления (рис. 2.5), м;
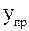 ,
, 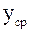 ,
, 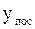 – предыдущая, средняя и последующая ординаты, определяемые по формулам:
– предыдущая, средняя и последующая ординаты, определяемые по формулам:
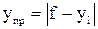 ; ;
|
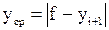 ; ;
|
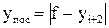 , ,
|
где
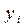 ,
, 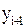 ,
, 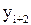 – измеренные последовательно ординаты от хорды через равные отрезки d, м;
– измеренные последовательно ординаты от хорды через равные отрезки d, м;
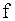 – ордината, расположенная на середине хорды.
– ордината, расположенная на середине хорды.
Установленные по формуле (2.1) фактические радиусы кривой в плане представляют собой перпендикуляры к касательным в трех точках и поэтому имеют плавающую вершину.
Если фактические радиусы кривой определять через отрезки 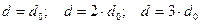 и т. д., то число вычисляемых радиусов (m) по трём ординатам определяется уравнением [4]
и т. д., то число вычисляемых радиусов (m) по трём ординатам определяется уравнением [4]
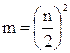 , ,
| (2.2) |
где n – число интервалов между измеренными ординатами, шт.
Так, для ординат, показанных на рис. 2.5, получаем следующее число радиусов кривой:
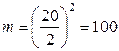 шт. шт.
|
 2015-05-30
2015-05-30 362
362








