Известно, что пересечение множеств A и B есть интервал числовой оси 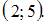 Тогда множества A и B могут быть равны …
Тогда множества A и B могут быть равны …

| 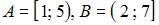
| ||

| 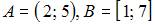
| ||
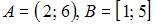
| |||
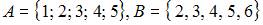
|
Решение:
Найдем пересечение предложенных множеств.
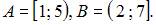 Полуинтервал
Полуинтервал 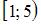 представляет собой часть числовой оси от точки 1 до точки 5, включающая точку 1 и не включающая точку 5. Полуинтервал
представляет собой часть числовой оси от точки 1 до точки 5, включающая точку 1 и не включающая точку 5. Полуинтервал 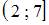 – это часть числовой оси от точки 2 до точки 7, не включающая точку 2 и включающая точку 7. Изобразим эти множества на рисунке:
– это часть числовой оси от точки 2 до точки 7, не включающая точку 2 и включающая точку 7. Изобразим эти множества на рисунке:

Пересечение множеств 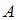 и
и 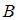 есть множество, состоящее из элементов, общих для обоих множеств. В нашем случае в него войдут точки числовой оси, принадлежащие обоим полуинтервалам
есть множество, состоящее из элементов, общих для обоих множеств. В нашем случае в него войдут точки числовой оси, принадлежащие обоим полуинтервалам 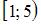 и
и 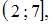 то есть все точки интервала
то есть все точки интервала 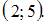 Таким образом,
Таким образом, 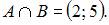
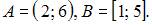 Интервал
Интервал 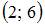 – это часть числовой оси от точки
– это часть числовой оси от точки 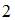 до точки
до точки 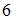 , не включающая точки
, не включающая точки 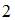 и
и 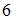 . Отрезок
. Отрезок 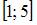 представляет собой часть числовой оси от точки
представляет собой часть числовой оси от точки 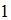 до точки
до точки 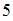 , включая точки
, включая точки 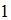 и
и 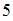 . Изобразим эти множества на рисунке:
. Изобразим эти множества на рисунке:

С помощью рисунка находим, что 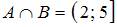 .
.
Если 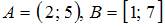 , то
, то

В этом случае 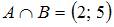 .
.
Если 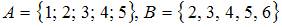 , то общими для обоих множеств будут элементы
, то общими для обоих множеств будут элементы 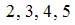 , то есть
, то есть 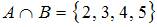 .
.
Таким образом, интервал числовой оси 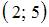 является пересечением множеств
является пересечением множеств 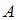 и
и 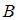 , если
, если 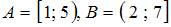 или
или 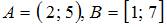 .
.
 2015-05-22
2015-05-22 557
557








