2015-05-22
1377
1. Бинарное отношение отцовства на множестве всех людей есть множество всех упорядоченных пар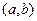 
таких, что a и b – люди и a – отец b.
2. Пусть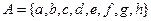 
и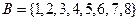 
, тогда подмножество 
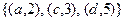в декартовом произведении 
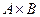является бинарным отношением между множествами А и В.
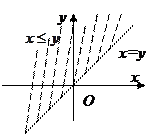3. На множестве целых чисел Z отношение делимости, состоящее из упорядоченных пар 
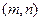, в которых m делится на n, является бинарным отношением. В этом случае обозначение mRn заменяется на m: n.
4. На множестве действительных чисел R упорядочение «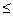
» – «меньше или равно» или «не больше» является бинарным отношением на R, состоящим из всех точек плоскости R 2, лежащих не ниже прямой x – y = 0 (см.рис.).
5. Для функции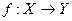 
ее график Г(f) = 
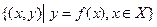является бинарным отношением между X и Y.
6. На множестве всех неотрицательных целых чисел Z+ = N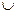 
{0} упорядочение «<» – «меньше» является бинарным отношением R, область определения которого – Z+, множество значений – Z+ \ {0}, обратным отношением 
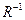к нему является отношение «>» – «больше».
Свойства бинарного отношения на множестве.
Определение 57. Бинарное отношение R на множестве А обладает свойством рефлексивности или называется рефлексивным, если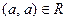 
для всех 
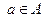, то есть для любого а этого множества элемент а находится в отношении R к самому себе.
Примеры рефлексивных отношений: равенство, одновременность, сходство.
Определение 58. Бинарное отношение R на множестве А обладает свойством антирефлексивности или называется антирефлексивным, если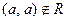 
для всех .
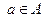Примеры нерефлексивных отношений: «заботиться о», «развлекать», «нервировать».
Определение 59. Бинарное отношение R на множестве А обладает свойством симметричности или называется симметричным, если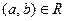 
влечет за собой 
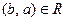для всех 
.
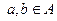Примером симметричных отношений могут быть: равенство «=», отношение эквивалентности, подобия, одновременности, некоторые отношения родства (например, отношение братства).
Определение 60. Бинарное отношение R на множестве А обладает свойством антисимметричности или называется антисимметричным, есл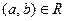и и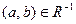 
влекут за собой 
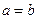для всех 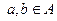, то есть R и R -1 выполняются одновременно лишь для равных между собой членов.
Определение 61. Бинарное отношение R на множестве А обладает свойством асимметричности или называется асимметричным, если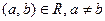 
, влечет за собой 
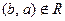для всех .
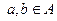Пример: отношение «больше» (>) и «меньше» (<). Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности.
Определение 62. Бинарное отношение R на множестве А обладает свойством транзитивности или называется транзитивным, есл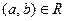и и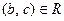 
влечет за собой 
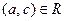для всех 
.
В противном случае отношение называется нетранзитивным.
Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее». Пример нетранзитивного отношения: «x отец y»
Определение 63. Бинарное отношение R на множестве А обладает свойством связанности или называется связанным, ес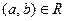ли или 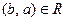для всех 
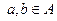, то есть, что для любых двух различных элементов a и b из множества A, одно из них находится в отношении R к другому.
Пример: отношение «меньше» (<).
