Множества

Введение в теорию множеств

Теоретико-множественные представления - описание иссле­дуемой системы, процессов средствами теории множеств, т.е. как множества взаимосвязанных и/или взаимодействующих частей - элементов. Связи между элементами задаются через отношения и/или соответствия. Множества, элементы, отношения, соот­ветствия характеризуются определенными свойствами и набо­ром допустимых операций над ними.

Состав объекта исследования может быть представлен в виде дискретного множества. Множество — основное поня­тие в теории множеств, которое вводится без определения.

Основные понятия

Множество— состоит из элементов. Принадлежность элемента а множеству М обозначается а М ("а принадлежит М "), непринадлежность - а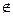М или а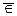М.

В А

Рисунок 1.1

Множество А называется подмножеством множества В (обозначается А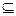В), если всякий элемент из А является элементом В (рис 1.1). Есл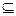и АВ и А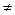В, то А называется строгим (собственным) подмножеством (обозначается А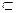В).

Примеры обозначения числовых множеств:

N – {1, 2, 3, …} – множество натуральных чисел,

N₀ – {0, 1, 2, 3, …} – множество неотрицательных целых чисел,

Z – {0, ±1, ±2, ±3, …} – множество целых чисел,

R – множество действительных чисел.

Два определения равенства множеств:

I. Множества А и В равны (А=В}, если их элементы совпадают.

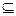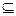П. Множества А и В равны, если АВ и ВА.

Множество, состоящее из конечного числа элементов, на­зывается конечным, в противном случае - бесконечным (например, множества N, R — бесконечные множества). Число элементов в конечном множестве М называется его мощностью и обозначается \М\.

Множество мощности 0, т.е. не содержащее элементов, называется пустым (обозначается Ø): |Ø| =0. Принято считать, что пустое множество является подмножеством любого множества.

Способы задания множеств:

• Перечислением, т.е. списком своих элементов. Списком можно задать лишь конечные множества. Обозначение списка - в фигурных скобках. Например, множество А устройств домашнего компьютера, состоящего из системного блока а, а также периферийных устройств В (монитора b, клавиатуры с и принтера d), может быть представлено списком:

А = {а, В} или А = {а, b, с, d}.

• Порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами мно­жества являются все объекты, которые могут быть построены с помощью такой процедуры.

Например, множество всех целых чисел, являющихся степенями двойки М₂ⁿ, nN, где N- множество натуральных чисел, (допустимое обозначение М₂ⁿ = 1, 2, 4, 8, 16,...) может быть представлено порождающей процедурой, заданной двумя правилами:

а) 1М₂ⁿ;

б) если тМ₂ⁿ _n, то 2тМ₂ⁿ

• Описанием характеристических свойств, которыми должны обладать его элементы; обозначается:

М= {х| Р(х)} или М= {х:P(x) }.

"Множество М состоит из элементов х таких, что х обладает свойством Р").

Например, множество А периферийных устройств персонального компьютера может быть определено:

А = {х: х - периферийное устройство персонального компьютера}.

Если свойство элементов множества М может быть опи­сано коротким выражением, это упрощает его символьное представление. Например, множество всех натуральных четных чисел М_2п может быть представлено:

М_2п = {х: х = 2п, nN}.

Пример 1. Задать различными способами множество N всех натуральных чисел: 1,2,3,...

Списком множество N задать нельзя ввиду его бесконечности.

Порождающая процедура содержит два правила:

а) 1N;

б) если nN, то n+1N.

Описание характеристического свойства элементов множества N:

N= {х:х- целое положительное число}.

Пример 2. Задать различными способами множество М всех четных чисел 2, 4, 6,..., не превышающих 100.

М_2n ={2,4,6,...,100}.

а)2 М_2n;

б) если nN, то (n+2)М_2n;

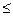в) n98.

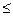М_2n = {п:п- целое положительное число, не превышающее 100} или М_2п = {п:пN и n/2N, n 100}.

Пример 3. Какие из приведенных определений множеств A, B, C, D являются корректными:

A ={1,2,3};

B ={5,6,6,7};

C= {х:хА};

D= { A,C }.

1. Определение множества A ={1,2,3} списком своих элементов формально корректно.

2. При перечислении элементов множества не следует указывать один и тот же элемент несколько раз. Корректное определение B ={5,6,7}.

3. Определение множества C= {х:хА} заданием характеристического свойства его элементов «принадлежать множеству А» корректно.

4. Определние списком множества D= { A,C } корректно.

Пример 4. Пары (1,2) и (2,1) не совпадают, хотя множества {1,2} и {2,1} равны.

Пример 5. Покажем, что множества М₁ = {x: sin x=1} и М₂ = {x: x=π/2+2kπ, k Z } совпадают.

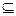Если хМ₁, то х является решением уравнения sin x=1. Но это значит, что х можно представить в виде x=π/2+2kπ и поэтому хМ₂. Таким образом, М₁ М₂. Если же хМ₂, т. е. x=π/2+2kπ, то sin x=1, т.е. М₂ 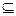М₁. Следовательно М₁=М₂.