2015-05-22
19755
Теорема: множество рациональных чисел является счётным.
Доказательство:
Необходимо доказать, что между множеством рациональных чисел и множеством натуральных чисел можно установить взаимо-однозначное соответствие. Для этого положительные рациональные числа запишем так:
1 строка: 1 2 3 4 5 6 7....
2 строка: ½ 2/2 3/2 4/2 5/2 6/2 7/2....
3 строка: 1/3 2/3 3/3 4/3............................
Таким образом, будет записано каждое положительное число. Например, число 7/31 будет записано в 31-й строке в 7-м столбце. Вообще, дробь m/n будет записана в n-й строке m-м столбце.
Для установления взаимно-однозначного соответствия теперь уже нельзя переходить от столбца к столбцу, потому что в каждом столбце содержится бесконечное множество элементов. Для доказательства этой теоремы будем использовать диагональный метод Кантора. Он заключается в том, что мы подходим к каждому рациональному числу и, следовательно, каждому рациональному числу будет поставлено в соответствие какое-либо натуральное число.
1 2 ½ 1/3 3........
|
|
|
↓ ↓ ↓ ↓ ↓
1 2 3 4 5..........
Так, с помощью диагонального метода устанавливаем взаимно-однозначное соответствие между множеством положительных рациональных и множеством натуральных чисел, а это значит, что множество положительных рациональных чисел счетно.
Также можно доказать, что множество отрицательных рациональных чисел счётно. Сложив эти два множества и прибавив к ним конечное множество, состоящее из элемента нуль, мы получим всё множество рациональных чисел.
Теорема. Множество всех действительных чисел несчетно.
Доказательство. Для доказательства достаточно установить, что множество действительных чисел интервала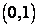 
образует несчетное множество. Допустим противное, что интервал 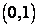есть счетное множество, т. е. все его точки можно перенумеровать:
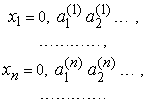
Но это предположение противоречиво. В самом деле, построим вещественное число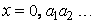 
, где цифры 
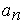подобраны так, чтобы 
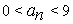и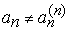 
. Ясно, что 
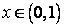, однако 
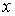не совпадает ни с одним из чисел 
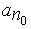, так как иначе должно было бы быть 
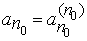, что не имеет места.
