Числовые множества. Множество натуральных чисел

Множество натуральных чисел. Числа, употребляемые для счета, называются натуральными (N= ).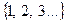

Множество целых чисел. Целые числа состоят из натуральных, нуля и чисел, противоположных натуральным (Z = ).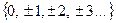

Множество рациональных чисел. Рациональными числами называются числа, которые представимы как 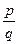, где p – целое, а q – натуральное (Q = ).

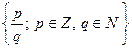Операции сложения: .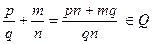

Операция умножения: .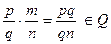

Свойства сложения:

1. .

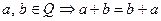2. .

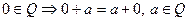3. 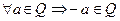, что .

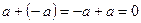4. 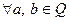существует и притом единственный 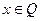, так что 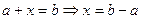(разность множеств).

5. Если 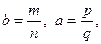то .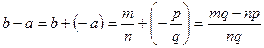

Свойства умножения:

1. .

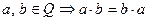2. 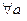существует единичный элемент, что .

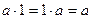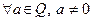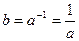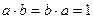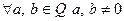3. существует такой элемент (обратное ему), что . 4. существует такой элемент 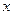, что 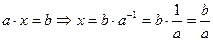. 5.Если .

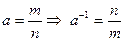Множество рациональных и иррациональных чисел

Всякое положительное рациональное число 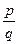разлагается в бесконечную периодическую десятичную дробь.

Верно и обратное утверждение:

Любая периодическая дробь есть десятичное разложение некоторого положительного рационального числа .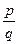

Всякая бесконечная непериодическая десятичная дробь называется иррациональным числом.

Иррациональное число нельзя представить в виде дроби 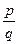и обратно, каждое число не представимое в виде 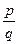является иррациональным.

Множество всех рациональных и иррациональных чисел обозначается символом R и называется множеством действительных чисел.

Над множествами действительных чисел можно провести все те же операции, что и над множеством рациональных чисел.