Операции над множествами

Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.

Множество обозначают символом A = { x }, где x - общее наименование элементов множества A. Часто множество записывают в виде A = { a, b, c,...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:

N - множество всех натуральных чисел;
Z - множество всех целых чисел;
Q - множество всех рациональных чисел;
R - множество всех действительных чисел;
C - множество всех комплексных чисел;
Z₀ - множество всех неотрицательных целых чисел.

Запись 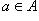(или 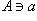) означает, что элемент a принадлежит множеству A.

Запись 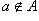(или 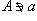) означает, что элемент a не принадлежит множеству A.

2. Множества натуральных, целых, рациональных и действительных чисел. Порядок арифметических действий над такими числами. Свойства дробей

1. Натуральные числа − числа, используемые при счете (перечислении) предметов:
N = {1, 2, 3,...}

2. Натуральные числа с включенным нулем − числа, используемые для обозначения количества предметов:
N ₀ = {0, 1, 2, 3,...}

3. Целые числа − включают в себя натуральные числа, числа противоположные натуральным(т.е. с отрицательным знаком) и ноль.
Целые положительные числа:
Z ⁺ = N = {1, 2, 3,...}
Целые отрицательные числа:
Z ⁻ = {..., −3, −2, −1}
Z = Z ⁻ ∪ {0} ∪ Z ⁺ = {..., −3, −2, −1, 0, 1, 2, 3,...}

4. Рациональные числа − числа, представляемые в виде обыкновенной дроби a / b, где a и b − целые числа и b ≠ 0.
Q = { x | x = a / b, a ∈ Z, b ∈ Z, b ≠ 0}
При переводе в десятичную дробь рациональное число представляется конечной или бесконечной периодической дробью.

5. Действительные (вещественные) числа − объединение рациональных и иррациональных чисел: R

6. Комплексные числа
C = { x+iy | x ∈ R и y ∈ R },
где i − мнимая единица.

7. N ⊂ Z ⊂ Q ⊂ R ⊂ C

К арифметическим или рациональным действиям над числами относят
сложение ,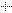
вычитание ,
умножение ,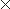
деление (или ).

Только два из этих действий — сложение и умножение — определены на множестве натуральных чисел .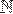

Действительно, деление и вычитание не всегда возможны на множестве .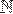
Например,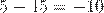
Разностью двух натуральных чисел и 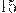является 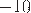, а это число не натуральное!
Скоро вы узнаете, что 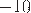является целым числом.

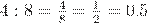
Частным двух натуральных чисел 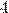и 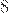является 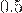, а это число не натуральное!
Скоро вы узнаете, что 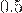является рациональным числом.

операции вычитания и деления НЕ ОПРЕДЕЛЕНЫ на множестве 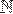, но это вовсе не значит, что вычитать и делить натуральные числа нельзя.

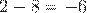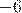( — число не натуральное).
НО 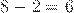( 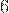— число натуральное).
Т.е. каждый раз мы с тобой брали разность и иногда выходили за пределы множества натуральных чисел (в примере выше мы получили целое число).

Определенной операцией называют операцию на некотором множестве, если ее выполнение НИКОГДА не выведет нас за пределы данного множества.

Так, сложение и умножение двух натуральных чисел ВСЕГДА будет числом натуральным, сколько бы раз мы эти операции не выполняли (в какой бы последовательности мы их не комбинировали).

Из натуральных чисел с помощью знаков арифметических действий и скобок составляют числовые выражения. Порядок выполнения арифметических действий в числовом выражении следующий:
вначале выполняют действия в скобках;
внутри любых скобок или в выражении без скобок сначала действия умножения и деления;
потом сложения и вычитания.

Например, если нужно найти значение выражения
,
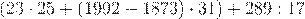то порядок выполнения арифметических действий такой:
1) Умножил 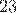на 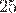, получил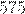
2) Подсчитал разность 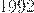и 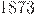, получил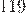
3) Значение этой разности (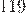) умножил на 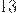и получил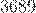
4) Сложил сумму, полученную в пункте 1) с произведением, полученным в пункте 3), т.е.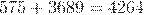
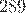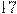5) Нашел результат деления на . Получил .
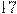6) Сложил результаты пунктов 5) и 4), получил .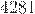

3. Числовая ось. Иррациональные, алгебраические и трансцендентные числа.

Числовая ось, или числовая прямая — это прямая, на которой выбраны:

• некоторая точка O — начало отсчёта;
• положительное направление, указанное стрелкой;
• масштаб для измерения длин.

Между вещественными числами и числовой осью устанавливаетсявзаимно однозначное соответствие: начало координат соответствуетнулю, числовое значение произвольной точки соответствуетрасстоянию её до начала координат — в положительном направлении со знаком плюс, иначе — со знаком минус.^[1] Таким образом, числовая ось состоит из точки начала координат и двух расходящихся от неё лучей, один из которых соответствуетположительным, а другой — отрицательным числам. Естественный порядок точек на прямой при таком соответствии согласуется с упорядоченностью чисел.

Иррациональные числа − числа, которые представляются в виде бесконечной непериодической десятичной дроби.

Алгебраи́ческое число́ над полем 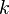— элемент алгебраического замыкания поля 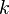, то есть корень многочлена (не равного тождественно нулю) с коэффициентами из .

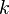Трансценде́нтное число́ (от лат. transcendere — переходить, превосходить) — это вещественное или комплексное число, не являющееся алгебраическим — иными словами, число, которое не может быть корнем многочлена с рациональными коэффициентами (не равного тождественно нулю).

4. Простейшие понятия исчисления высказываний и предикатов. Необходимые и достаточные условия.

Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектомвысказывания называется то, о чём делается утверждение.

Предикат в программировании — функция, принимающая один или более аргументов и возвращающая значения булева типа.

Далее в этой статье слово предикат используется в значениивысказывательной формы.

5. Общее определения функций (отображений) функционалов, числовых последовательностей. Классификация отображений (однозначные, многозначные, биективные, сюрьективные, инъективные отображения).

Функциона́л — это отображение, заданное на произвольном множестве и имеющее числовую область значений: обычно множество вещественных чисел 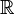иликомплексных чисел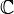

Область определения функционала может быть любым множеством. Если область определения является топологическим пространством, можно определитьнепрерывный функционал; если область определения является линейным пространством над 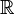или над 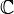, можно определить линейный функционал; если область определения является упорядоченным множеством, можно определить монотонный функционал.

Функционал, заданный на топологическом пространстве 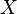, называется непрерывным, если он непрерывен как отображение в топологическое пространство 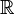или .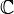

Функционал, заданный на топологическом пространстве 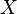, называется непрерывным в точке 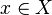, если он непрерывен в этой точке как отображение в топологическое пространство 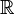или .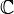

В более широком смысле функционалом называется любое отображение из произвольного множества в произвольное (не обязательно числовое) кольцо.

Функционал, заданный на линейном пространстве, и сохраняющий сложение и умножение на константу, называется линейным функционалом. (Отображение линейного пространства в линейное пространство называют оператором).

Пожалуй, самый простой функционал — проекция - (сопоставление вектору одной из его компонент или координат).

Довольно часто в роли линейного пространства выступает то или иное пространство функций (непрерывные функции на отрезке, интегрируемые функции на плоскости и т.д.). Поэтому в прикладных областях под функционалом часто понимают функцию от функций, отображение, переводящее функцию в число (действительное или комплексное).

Функционал на линейном пространстве называется положительно определённым, если его значение неотрицательно и равно нулю только в нуле.

Отображение, переводящее вектор в его норму, является выпуклым положительно определённым функционалом, это один из самых распространённых функционалов. В физике часто используется действие — тоже функционал.

Задачи оптимизации формулируются на языке функционалов: найти решение (уравнения, системы уравнений, системы ограничений, системы неравенств, системы включений и т. п.), доставляющее экстремум (минимум или максимум) заданному функционалу. Функционалы также рассматриваются в вариационном анализе.

6. Определение элементарных функций, их свойства, графики.

математическое понятие, отражающее связь между элементамимножеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемогообластью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной 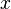однозначно определяет значение выражения 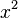, а значение месяцаоднозначно определяет значение следующего за ним месяца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

7. Алгебраические операции и их классификация. Множество комплексных чисел, их геометрическая интерпретация. Операция над комплексными числами