2015-05-22
783
Над множествами можно проводить ряд действий:
1. Объединение – множество C, включающее в себя все элементы из A и все элементы из B. Обозначение: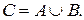 
2. Пересечение – множество C, включающее в себя все элементы, принадлежащие одновременно множеству A и множеству B. Обозначение: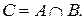 
3. Вычитание – множество C, включающее в себя все элементы из A, не принадлежащие множеству B. Обозначение: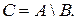 
Часто при включении 
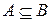вместо 
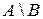пишут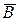 
и говорят о дополнении подмножества B.
4. Произведение – множество C, включающее в себя все упорядоченные пары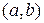 
, где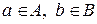 
. Обозначение: 
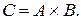Если 
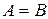, то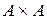 
называется декартовым квадратом множества A; подмножество всевозможных элементов 
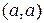во множестве 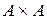называется диагональю множества A и обозначается 
.
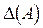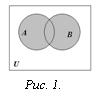
Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
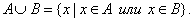
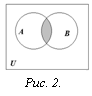
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
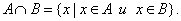
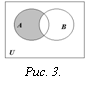
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):
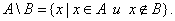
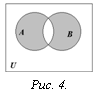
Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
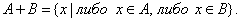
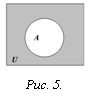
Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):
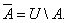
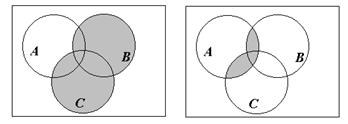
Пример 5. С помощью диаграмм Эйлера – Венна проиллюстрируем справедливость соотношения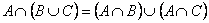 
(рис. 6).
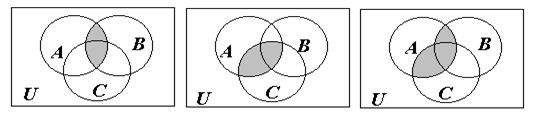
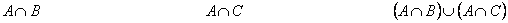
Рис. 6.
Убедились, что в обоих случаях получаем равные множества. Следовательно, исходное соотношение справедливо.
