Для расчета дисперсии упрощенным способом используют её свойства. При этом последовательно выполняется ряд шагов:
1. Выбирается условный нуль – вариант, находящийся в середине ряда распределения или вариант с наибольшей частотой.
2. Все значения признака уменьшаются на величину А – условный нуль, т.е. находится отклонение вариантов признака от условного нуля.
3. Все отклонения значений от условного нуля уменьшаются в k раз, часто за k принимают величину интервала или значение, кратное величине отклонения. В результате этих действий получают ряд распределения от условной величины 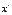 ,равной
,равной 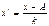
4.Исчисляют условную среднюю 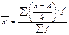
5.Исчисляют среднюю из квадратов условных величин
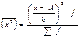
6.Исчисляется условная дисперсия.
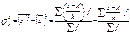
7.Исчисляется дисперсия от величины х:
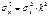
Пример:
| % выполнения норм выработки | Число рабочих, чел | х | а=125 х - А |
| 90-100 | -30 | ||
| 100-110 | -20 | ||
| 110-120 | -10 | ||
| 120-130 | |||
| 130-140 | |||
| 140-150 | |||
| 150-160 | |||
| 160-170 | |||
| 170-180 | |||
| Итого | - | - |
K=10
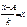
| 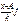
| 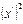
| 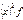
|
| -3 | -6 | ||
| -2 | -12 | ||
| -1 | -8 | ||
| - | - |
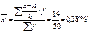

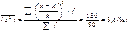
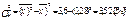
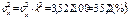
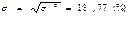
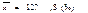
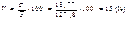
 2015-06-10
2015-06-10 588
588








