Пусть 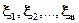 - последовательность независимых случайных величин, дисперсии которых ограничены одним и тем же числом c:
- последовательность независимых случайных величин, дисперсии которых ограничены одним и тем же числом c: 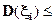 c, i=1,2..,n Тогда при n → ∞ и для любого
c, i=1,2..,n Тогда при n → ∞ и для любого 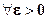
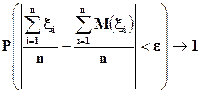
Это утверждение можно записать иначе, в эквивалентной форме.
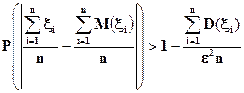 , (33)
, (33)
которую используют при решении прикладных задач.
В частности, отсюда следует утверждение:
Если 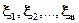 - последовательность попарно независимых случайных величин с одинаковым математическим ожиданием a и дисперсией σ2, то при n → ∞ и для любого
- последовательность попарно независимых случайных величин с одинаковым математическим ожиданием a и дисперсией σ2, то при n → ∞ и для любого 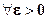
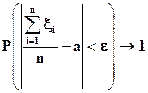 ,
,
или в эквивалентной форме
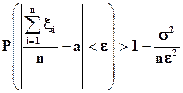 (34)
(34)
Теорема Бернулли.
Применим теорему Хинчина к случайной величине 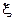 = m – число появлений события А в серии n независимых испытаний. Представим эту случайную величину в виде суммы попарно независимых, одинаково распределенных случайных величин
= m – число появлений события А в серии n независимых испытаний. Представим эту случайную величину в виде суммы попарно независимых, одинаково распределенных случайных величин 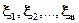 ,
,
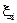 =
= 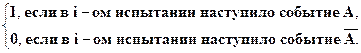
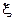 = m =
= m = 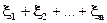 (35)
(35)
Вероятности р(А) = р,р (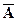 ) = 1 - р = q,М (
) = 1 - р = q,М ( 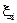 ) = р,D (
) = р,D ( 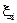 ) = pq. Тогда при
) = pq. Тогда при
n → ∞ и для любого 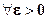
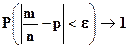 ,
,
или в эквивалентной форме
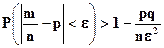 . (36)
. (36)
Смысл этой теоремы заключается в том, что относительная частота появления события по вероятности сходится к вероятности этого события.
Обобщением теоремы Бернулли на случай, когда испытания происходят при неодинаковых условиях, что вызывает изменение вероятности появлений события А в каждом испытании, является теорема Пуассона.
Теорема Пуассона.
Рассмотрим последовательность n независимых испытаний, в каждом из которых событие А наступает с вероятностью р 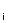 , i=1,2,…n. Рассуждая также,
, i=1,2,…n. Рассуждая также,
как и в предыдущем случае, получим М ( 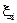 ) = р
) = р 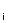 ,D (
,D ( 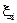 ) =р
) =р 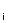 q
q 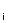 .По теореме Чебышева получим
.По теореме Чебышева получим
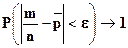 , где
, где 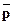 =
= 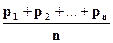 , т.е. относительная частота появления события А сходится по вероятности к средней арифметической вероятностей этого события в каждом испытании.
, т.е. относительная частота появления события А сходится по вероятности к средней арифметической вероятностей этого события в каждом испытании.
Запишем утверждение теоремы Пуассона в эквивалентной форме
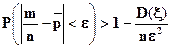 ,
,  (37)
(37)
где 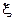 = m =
= m = 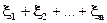 , а
, а 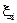 (i=1,2,..n) определены выражением (35).
(i=1,2,..n) определены выражением (35).
Рассмотрим пример на применение закона больших чисел.
Пример 17. из 100 изделий, отправляемых в сборочный цех, было подвергнуто обследованию 200, отобранных случайным образом. Среди них оказалось 25 бракованных. Приняв долю бракованных изделий среди отобранных, за вероятность изготовления бракованного изделия, оценить вероятность того, что
во всей партии бракованных изделий окажется в пределах от 15% до 20%.
Для решения задачи используем неравенство (36). Вероятность изготовления бракованного изделия по условию 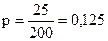 .Требуется найти вероятность
.Требуется найти вероятность
Р(0,10 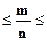 0,15). Вычтем в каждой части неравенства р, получим
0,15). Вычтем в каждой части неравенства р, получим
Р(0,10 – 0,125 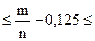 0,15– 0,125) = Р(– 0,025
0,15– 0,125) = Р(– 0,025 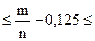 0,025) или
0,025) или
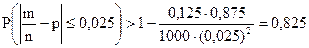 .
.
Первое неравенство Чебышева.
Если случайная величина 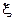 имеет конечный первый абсолютный момент
имеет конечный первый абсолютный момент
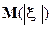 , то
, то 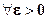
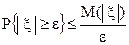 . (38)
. (38)
В частности, если 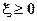 и существует
и существует 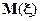 , то
, то
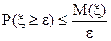 . (39)
. (39)
 2015-06-10
2015-06-10 745
745








