Определение 2.9. Назовем класс A подмножеств пространства 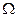 алгеброй множеств, если
алгеброй множеств, если
1) 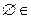 A,
A, 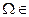 A;
A;
2) если 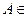 A, то и
A, то и 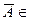 A;
A;
3) если 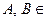 A, то и
A, то и 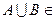 A,
A, 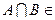 A.
A.
Определение 2.10. Алгебра множеств A называется 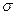 - алгеброй, если из того, что
- алгеброй, если из того, что 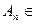 A,
A, 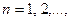 следует, что
следует, что 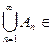 A,
A, 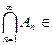 A.
A.
Определение 2.11. Тройку (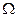 , A, Р), где
, A, Р), где 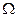 - пространство элементарных событий, A –
- пространство элементарных событий, A – 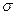 -алгебра подмножеств
-алгебра подмножеств 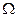 , Р – числовая функция, определенная на событиях и называемая вероятностью, будем называть вероятностным пространством, если выполнены следующие аксиомы:
, Р – числовая функция, определенная на событиях и называемая вероятностью, будем называть вероятностным пространством, если выполнены следующие аксиомы:
А1. 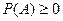 для всех
для всех 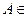 A (неотрицательность Р);
A (неотрицательность Р);
А2. 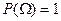 (нормированность Р);
(нормированность Р);
А3. 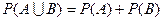 , если
, если 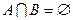 (аддитивность Р);
(аддитивность Р);
А4. Если 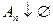 , то есть
, то есть 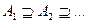 и
и 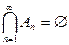 , то
, то 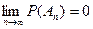 (непрерывность Р).
(непрерывность Р).
Из этих аксиом вытекают следующие свойства вероятности:
1) Если 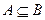 , то
, то 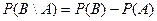 ;
;
2) Если 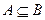 , то
, то 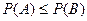 ;
;
3) Для любого 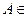 A
A 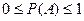 ;
;
4) 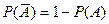 ;
;
5) 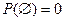 .
.
 2015-06-10
2015-06-10 533
533








