Рассмотрим конечное вероятностное пространство. В этом случае 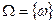 – конечное пространство, A – алгебра всех подмножеств множества
– конечное пространство, A – алгебра всех подмножеств множества 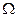 (ввиду конечности A эта алгебра автоматически представляет собой
(ввиду конечности A эта алгебра автоматически представляет собой 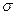 -алгебру). Вероятность
-алгебру). Вероятность 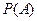 для любого подмножества
для любого подмножества 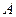 из
из 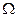 в этом случае можно задать следующим образом. Пусть заданы неотрицательные числа
в этом случае можно задать следующим образом. Пусть заданы неотрицательные числа 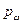 такие, что
такие, что 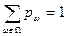 . Вероятность
. Вероятность 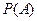 определим как сумму
определим как сумму
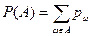 .
.
Легко видеть, что так определенная вероятность (вместе с 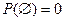 ) удовлетворяет всем аксиомам А1. – А4. Обозначим
) удовлетворяет всем аксиомам А1. – А4. Обозначим 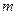 – число элементов в множестве
– число элементов в множестве 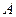 ,
, 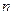 – число элементов в множестве
– число элементов в множестве 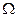 . В случае, когда все элементарные исходы
. В случае, когда все элементарные исходы 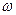 равновозможные, то есть все
равновозможные, то есть все 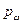 равны друг другу, получаем классическое определение вероятности. Так как
равны друг другу, получаем классическое определение вероятности. Так как 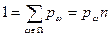 , то
, то 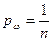 и
и
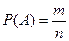 . . | (2.1) |
Таким образом, вероятность события 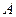 – это отношение числа элементарных исходов, благоприятствующих событию
– это отношение числа элементарных исходов, благоприятствующих событию 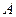 , к общему числу элементарных исходов.
, к общему числу элементарных исходов.
Пример 2.8. В программе для компьютера, написанной в Турбо Паскале, использована функция 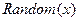 , генерирующая целые числа от 1 до х. Какова вероятность того, что при выполнении этой функции появится число, делящееся на 5, если х=100?
, генерирующая целые числа от 1 до х. Какова вероятность того, что при выполнении этой функции появится число, делящееся на 5, если х=100?
Решение. Обозначим событие: А – при значении х=100 появится число, делящееся на 5. Найдем вероятность события А, применив формулу (2.1).
При х=100 может появиться любое из 100 имеющихся целых чисел, следовательно, общее число исходов испытания 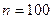 .
.
Для того, чтобы найти число исходов благоприятствующих событию А, воспользуемся признаком делимости чисел на 5. На 5 делятся числа, оканчивающиеся цифрами 0 или 5. Среди 100 целых чисел есть 20 таких чисел, следовательно, 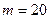 .
.
Вероятность события А равна
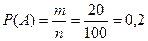 .
.
Пример 2.9. Ребенок играет с буквами разрезной азбуки. Какова вероятность того, что, разложив в ряд буквы К, И, Р, Д, А, Н, З, П, он составит слово ПРАЗДНИК?
Решение. Обозначим событие: А – ребенок составит слово ПРАЗДНИК. Найдем вероятность события А, применив формулу (2.1).
Общее число исходов испытания получим, используя формулы комбинаторики. Всего имеется 8 элементов – 8 букв, нас интересуют различные перестановки из этих элементов, следовательно, 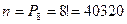 .
.
Число исходов испытания, благоприятствующих событию А, равно 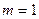 , так как требуется составить слово с буквами, расставленными в определенном порядке, и эти буквы различны.
, так как требуется составить слово с буквами, расставленными в определенном порядке, и эти буквы различны.
Вероятность события А равна
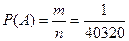 .
.
Пример 2.10. В ящике 15 деталей, среди которых 10 окрашены. Сборщик наудачу выбрал 3 детали. Найти вероятность того, что все выбранные детали окрашены.
Решение. Обозначим событие: А – все три выбранные детали окрашены. Найдем вероятность события А, применив формулу (2.1).
Общее число исходов испытания получим, используя формулы комбинаторики. Испытание заключается в выборе 3 деталей из 15 имеющихся. Таким образом, общее число исходов – это число всевозможных наборов по 3 элемента, которые можно составить из множества, состоящего из 15 элементов, не учитывая порядок, то есть 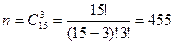 .
.
Число исходов испытания, благоприятствующих событию А, равно числу всевозможных наборов по 3 детали, которые можно составить из множества окрашенных деталей, то есть 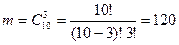 .
.
Вероятность события А равна 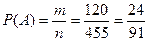 .
.
Пример 2.11. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.
Решение. Обозначим событие: А – среди отобранных студентов 5 отличников. Найдем вероятность события А, применив формулу (2.1).
Здесь 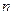 – общее число способов выбора 9 студентов из 12,
– общее число способов выбора 9 студентов из 12, 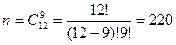 .
.
Число исходов испытания, благоприятствующих событию А, вычисляем по правилу произведения 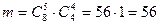 , где
, где 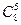 – число возможных наборов из 8 отличников по 5,
– число возможных наборов из 8 отличников по 5, 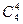 – число возможных наборов по 4 из остальных студентов.
– число возможных наборов по 4 из остальных студентов.
Вероятность события А равна
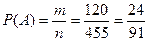 .
.
 2015-06-10
2015-06-10 11491
11491








