Расчетное задание №3

2.

3.

3.1. В прямоугольник 5×4 см² вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?

3.2. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?

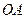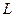3.3. На отрезок длины числовой оси 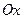наудачу поставлена точка 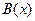. Найти вероятность того, что меньший из отрезков 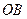и 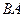имеет длину, большую .

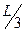3.4. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями.

3.5. В круг радиуса 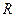наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри правильного треугольника, вписанного в круг.

3.6. Из отрезка [0, 2] наудачу выбраны два числа 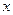и 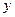. Найдите вероятность того, что эти числа удовлетворяют неравенствам .

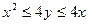3.7. Молодой человек и девушка договорились встретиться в 12ч. Каждый может придти от 12 до 13 ч. Договорились ждать 20 минут. Какова вероятность того, что они встретятся?

3.8. В квадратном трехчлене 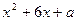коэффициент 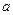по модулю не больше 10. Он выбирается наудачу. Какова вероятность того, что трехчлен будет иметь вещественные корни?

3.9. В круге произвольно выбирается точка. Какова вероятность того, что ее расстояние до центра круга больше половины?

3.10. Самолет бомбит мост размером 20м на 9м. Зона бомбометания: эллипс с полуосями 150м и 200м. Найти вероятность попадания бомбы в мост.

3.11. Точку случайным образом бросают в круг радиуса 1. Какова вероятность того, что точка попадет во вписанный в круг квадрат?

3.12. Наудачу выбирают 2 числа из промежутка [0,1]. Какова вероятность, что их произведение меньше .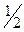

3.13. Из промежутка [0,1] выбрали наудачу два числа. Какова вероятность, что их сумма больше либо равна 1, а их разность меньше либо равна 0?

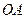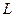3.14. На отрезок длины числовой оси 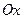наудачу поставлена точка 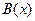. Найти вероятность того, что меньший из отрезков 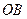и 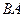имеет длину, большую .

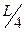3.15. Внутри эллипса 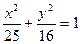расположен круг 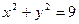. Найти вероятность попадания точки в кольцо, ограниченное эллипсом и кругом.

3.16. В треугольник с вершинами (-1,0), (0,1), (1,0) наудачу брошена точка (х,у). Найти вероятность того, что координаты точки удовлетворяют неравенству .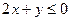

3.17. На отрезке 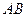длиной 2 наудачу выбраны две точк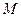и и 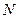. Найти вероятность того, что площадь круга, построенного на диаметре 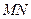не превзойдет .

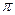3.18. Наудачу выбираю два числа из промежутка [-1,1]. Какова вероятность, что их сумма больше 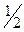, а произведение отрицательно.

3.19. На отрезок 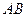брошена точка 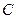. Найти вероятность того, что произведение длин отрезков 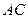и 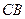больше .

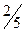3.20. Наугад берутся два числа из отрезка [0,2]. Найти вероятность того, что их сумма больше двух, а сумма их квадратов меньше 4.

3.21. Компьютер сгенерировал два числа из промежутка [-1,2]. Какова вероятность, что их сумма больше 1, а произведение меньше 1?

3.22. Приемник и передатчик выходят в эфир в течение часа в любой момент времени и дежурят по 15 минут. Какова вероятность приема информации?

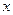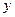3.23. Наудачу взяты два положительных числа и , каждое из которых не превышает двух. Найти вероятность того, что их произведение 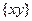будет не больше единицы, а частное от деления 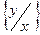– не больше двух.

3.24. На плоскости проведены параллельные прямые на расстоянии 8см друг от друга. Найти вероятность того, что наудачу брошенный на эту плоскость круг радиуса 3 см не будет накрывать ни одну линию.

3.25. Найти вероятность того, что сумма двух наугад взятых положительных чисел не превзойдет единицы, а их произведение будет не больше 3/16, если каждое из этих чисел не больше единицы.