Еще один важный класс моделей вероятностных пространств дают так называемые геометрические вероятности. Пусть 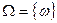 – область евклидова n-мерного пространства с конечным n-мерным объемом. Событиями назовем подмножества
– область евклидова n-мерного пространства с конечным n-мерным объемом. Событиями назовем подмножества 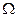 , для которых можно определить n-мерный объем. За множество событий можно принять так называемую
, для которых можно определить n-мерный объем. За множество событий можно принять так называемую 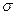 -алгебру B борелевских подмножеств
-алгебру B борелевских подмножеств 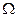 . За вероятность события
. За вероятность события 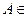 B примем
B примем
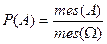 , , | (2.2) |
где 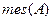 – мера множества
– мера множества 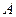 (длина, площадь, объем и т.д., в зависимости от размерности того пространства, в котором рассматриваются данные множества).
(длина, площадь, объем и т.д., в зависимости от размерности того пространства, в котором рассматриваются данные множества).
В частности, можно выделить следующие три случая.
1. Пусть отрезок 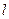 составляет часть отрезка
составляет часть отрезка 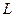 . На отрезок
. На отрезок 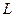 наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок
наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок 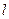 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка
пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 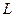 , то вероятность попадания точки на отрезок
, то вероятность попадания точки на отрезок 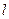 определяется равенством
определяется равенством
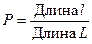 . . | (2.3) |
2. Пусть плоская фигура 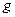 составляет часть плоской фигуры
составляет часть плоской фигуры 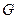 . На фигуру
. На фигуру 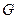 наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру
наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру 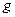 пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно
пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно 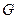 , ни от формы
, ни от формы 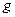 , то вероятность попадания точки в фигуру
, то вероятность попадания точки в фигуру 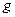 определяется равенством
определяется равенством
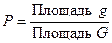 . . | (2.4) |
3. Аналогично определяется вероятность попадания точки в пространственную фигуру 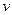 , которая составляет часть фигуры
, которая составляет часть фигуры 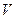 :
:
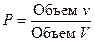 . . | (2.5) |
Пример 2.12. На отрезок 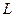 , имеющий длину 40 см, помещен меньший отрезок
, имеющий длину 40 см, помещен меньший отрезок 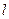 длиной 15 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок.
длиной 15 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок.
Решение. Обозначим событие: А – точка, наудачу поставленная на отрезок 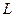 , попадет также и на отрезок
, попадет также и на отрезок 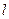 .
.
Найдем вероятность события А, применив формулу (2.3).
Вероятность события А равна 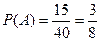 .
.
Пример 2.13. Внутрь круга радиуса 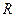 брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника.
брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника.
Решение. Обозначим событие: А – точка, наудачу брошенная в круг, окажется внутри вписанного в этот круг правильного треугольника.
Найдем вероятность события А, применив формулу (2.4).
Площадь круга радиуса 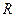 равна
равна 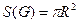 . Площадь вписанного в круг правильного треугольника равна
. Площадь вписанного в круг правильного треугольника равна 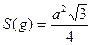 , где
, где 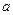 - сторона треугольника. Кроме того,
- сторона треугольника. Кроме того, 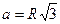 , поэтому
, поэтому 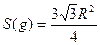 . Следовательно, вероятность события А равна
. Следовательно, вероятность события А равна
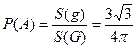 .
.
Пример 2.14 (Задача о встрече). Два товарища условились встретиться в определенном месте между 12 часами и половиной первого дня. Пришедший первым ждет первым ждет другого в течение 20 минут, после чего уходит. Найти вероятность того, что встреча товарищей состоится, если каждый из них наудачу выбирает момент своего прихода (в промежутке от 12 часов до половины первого) и моменты прихода обоих независимы.
Решение. Обозначим событие: А – встреча товарищей состоится.
Найдем вероятность события А, применив формулу (2.4).
Обозначим момент прихода одного из них через x (мин), а момент прихода другого через y (мин). Тогда время прихода товарищей можно отождествить с точкой 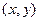 декартовой плоскости. Все возможные исходы испытания изображаются точками квадрата:
декартовой плоскости. Все возможные исходы испытания изображаются точками квадрата: 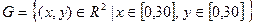 , площадь которого
, площадь которого 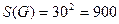 .
.
Для того чтобы встреча произошла, необходимо и достаточно, чтобы выполнялось условие: 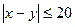 . Исходы испытания, благоприятствующие событию А, можно определить множеством:
. Исходы испытания, благоприятствующие событию А, можно определить множеством: 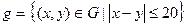 (рис. 5).
(рис. 5).
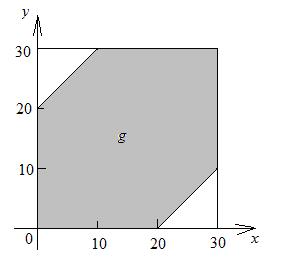 | 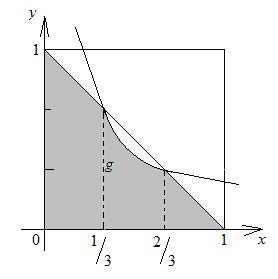 |
| рис. 5 | рис. 6 |
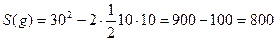 .
.
Следовательно, вероятность события А равна
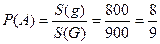 .
.
Пример 2.15. Наудачу взяты два неотрицательных числа 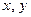 , каждое их которых не больше единицы. Найти вероятность того, что их сумма окажется меньше либо равна 1, а произведение – не больше
, каждое их которых не больше единицы. Найти вероятность того, что их сумма окажется меньше либо равна 1, а произведение – не больше 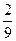 .
.
Решение. Обозначим событие: А – сумма наудачу взятых чисел 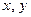 меньше либо равна 1, а произведение – не больше
меньше либо равна 1, а произведение – не больше 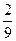 .
.
Найдем вероятность события А, применив формулу (2.4).
Множество элементарных исходов можно отождествить с точками квадрата: 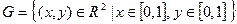 , площадь которого
, площадь которого 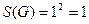 .
.
Исходы испытания, благоприятствующие событию А, можно определить множеством: 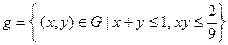 . Вычислим площадь области
. Вычислим площадь области 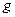 :
:
Найдем абсциссы точек пересечения прямой 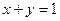 и гиперболы
и гиперболы 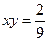 :
:
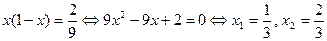 ,
,
откуда, 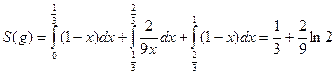 .
.
Следовательно, вероятность события А равна
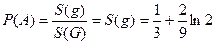 .
.
 2015-06-10
2015-06-10 1615
1615
