Отображения вероятностных пространств

Дадим формальное определение отображения вероятностного пространства в измеримое пространство

Пусть

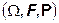
основное вероятностное пространство

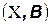
измеримое пространство

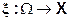
поточечное отображение (функция), ставящее в соответствие каждому элементарному исходу основного пространства точку x пространства X.

Отображение

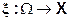
называется измеримое отображение, если

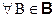
множество (прообраз B)

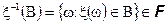
Покажите, что так определенная функция будет вероятностью

Измеримость отображения гарантирует, что функция

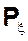
определенная на сигма-алгебре

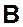
по формуле

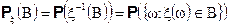
будет вероятностью.

Эта функция называется распределение, индуцированное отображением

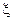
или просто распределение

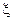
Таким образом с каждым отображением

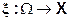
связано новое вероятностное пространство

.

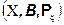Докажите это!

Заметим также, что совокупность прообразов всех множеств из Bобразует сигма-алгебру, которая обозначается 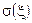и называется сигма-алгебра, порожденная отображением

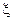
Мы часто будем пользоваться отображениями пространств, так как каждое такое отображение указывает связь между различными математическими моделями.