Следующая теорема дает пример применения предыдущей теоремы для доказательства сходимости относительной частоты события к его вероятности в схеме Бернулли.
Закон больших чисел в форме Бернулли
Пусть 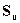 - число успехов в n испытаниях по схеме Бернулли с вероятностью успеха p. Тогда
- число успехов в n испытаниях по схеме Бернулли с вероятностью успеха p. Тогда
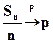
Доказательство.
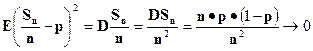
Доказательство завершено.
Таким образом, для доказательства слабой сходимости достаточно доказать сходимость по вероятности или в среднеквадратическом.
При доказательстве теорем о слабой сходимости используется также следующая важная теорема.
Теорема ({Хелли-Брея).
Пусть
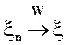
и
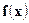
- непрерывная ограниченная функция. Тогда
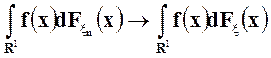 .
.
 2015-06-10
2015-06-10 505
505








