Теорема (Обратная теорема Хелли-Брея)

Пусть для любой

непрерывной ограниченной функции

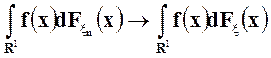
Тогда

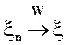
Доказательство.

Идея доказательства аналогична идее доказательства предыдущей теоремы и основана на возможности приблизить ступенчатую функцию 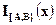непрерывной функцией 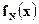. Действительно, опять выбирая подходящие точки непрерывности и полагая

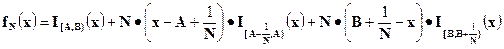видим, что близкие между собой интегралы

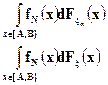
можно сделать сколь угодно близкими, соответственно. к интегралам

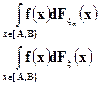
Теорема доказана.

Так как

,

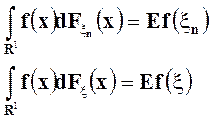то последние две теоремы дают необходимые и достаточные условия слабой сходимости в терминах сходимости математических ожиданий от непрерывных ограниченных функций.