Доказательство. Любую непрерывную на всей прямой функцию можно сколь угодно точно приблизить линейной комбинацией ступенчатых функций на любом интервале [-A,A)

Любую непрерывную на всей прямой функцию 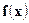можно сколь угодно точно приблизить линейной комбинацией ступенчатых функций на любом интервале [-A,A), A>0.

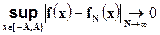
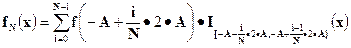
Выберем A так, чтобы точки –A, A и точки разбиения

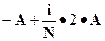
были бы точками непрерывности функции распределения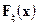

Тогда интегралы

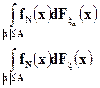
одинаковым образом выражаются через значения функций распределения 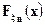и 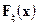и могут быть сделаны сколь угодно близкими выбором достаточно большого n. Следовательно, близки и интегралы

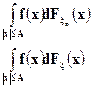
Так как функция 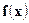ограничена, то выбором достаточно большого A можно сделать сколь угодно малыми интегралы

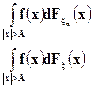
Теорема доказана.

Верна и обратная теорема.