Пусть 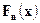 - произвольная последовательность функций распределения. Тогда существует подпоследовательность последовательности
- произвольная последовательность функций распределения. Тогда существует подпоследовательность последовательности 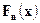 , которая сходится во всех точках непрерывности к некоторой предельной неубывающей непрерывной слева функции
, которая сходится во всех точках непрерывности к некоторой предельной неубывающей непрерывной слева функции 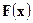 .
.
Заметим, что функция 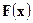 не обязательно является функцией распределения, но (очевидно) обязательно является неубывающей функцией, такой что
не обязательно является функцией распределения, но (очевидно) обязательно является неубывающей функцией, такой что
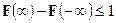
(несобственной функцией распределения).
Например, последовательность функций распределения 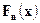 случайных величин
случайных величин 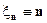 сходится при
сходится при 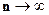 к функции
к функции 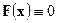
Теорема непрерывности для характеристических функций.
Для того, чтобы
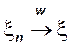
необходимо и достаточно, чтобы для всех t
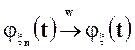
 2015-06-10
2015-06-10 346
346








