2015-06-10
331
Пусть
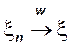
Тогда используя ограниченность, непрерывность по x для любого t функции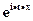 
и теорему Хелли-Брея получаем
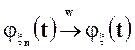
Доказательство необходимости завершено.
Пусть теперь
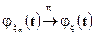
Тогда, используя теорему о выборе, мы можем извлечь из любой подпоследовательности последовательности функций распределения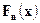 
случайных величин 
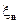, сходящуюся к некоторой функции 
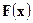подпоследовательность 
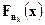, при этом соответствующая подпоследовательность характеристических функций 
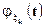как подпоследовательность сходящейся последовательности характеристических функций сходится к 
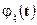. Покажем, что функция 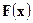является функцией распределения.
Полагая
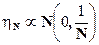
и применяя к паре функций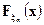 
, 
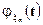равенство Парсеваля
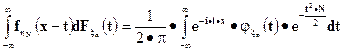
получаем, что, с одной стороны, для любого x
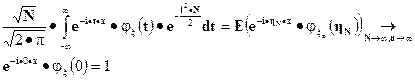
С другой стороны, для любых N, n и х
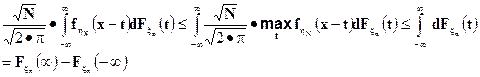
Таким образом:
1. Функция 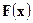является собственной функцией распределения
2. Из любой подпоследовательности последовательности функций распределения 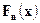случайных величин 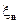можно извлечь сходящуюся к 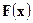подпоследовательность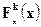 
3. Характеристическая функция 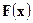совпадает с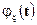 
·
Используя теорему единственности для характеристических функций получаем из 1) и 3), что функци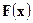и и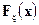 
совпадают и из 2) следует утверждение второй части теоремы (доказательство от противного).
