Преобразуем формулу
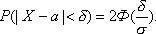
Введем обозначение
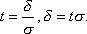
Тогда получим:
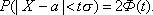
Если t=3, то
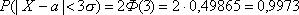
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально
Непрерывная случайная величина X называется распределенной по показательному закону, если ее плотность распределения вероятности имеет вид:
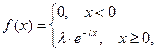
где 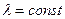 ,
, 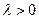 - параметр распределения.
- параметр распределения.
Функция распределения показательного распределения имеет вид:
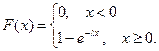
Графики функции распределения 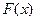 и функции плотности
и функции плотности 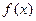 представлены на рисунках, соответственно.
представлены на рисунках, соответственно.
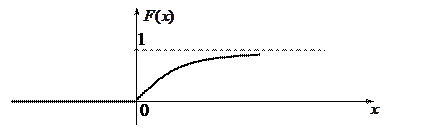
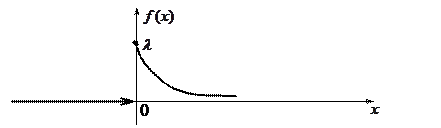
Числовые характеристики случайной величины, распределенной по показательному закону, вычисляются по формулам:
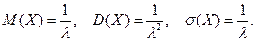
К показательному распределению приводят задачи о длительности безаварийной работы различных машин и приборов, оно играет особую роль в теории массового обслуживания и надежности, в страховом деле, демографии и многих других прикладных дисциплинах.
Пример. Случайная величина х - время работы радиолампы — имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 ч, если среднее время работы радиолампы 400 ч.
Решение. По условию задачи математическое ожидание случайной величины х- равно 400 ч, следовательно, 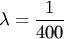 . Искомая вероятность есть
. Искомая вероятность есть
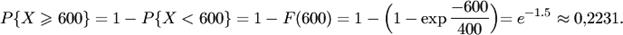
Задачи
1.Совместная плотность распределения двумерной случайной величины {X,Y} равна
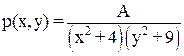 .
.
Найти: неизвестную константу А, функцию распределения {X,Y}.
2.Даны плотности вероятности независимых составляющих двумерной случайной величины (X, Y):
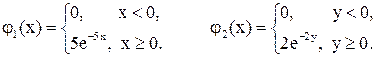
Найти выражение совместной плотности и функции распределения двумерной случайной величины.
3.По заданной функции распределения 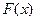 найти функцию плотности
найти функцию плотности 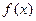 , построить графики
, построить графики 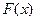 и
и 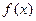 , найти
, найти 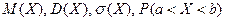 .
.
А) 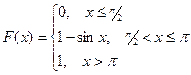
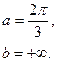
Б) 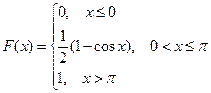
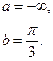
В) 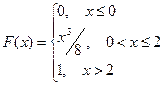
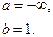
Г) 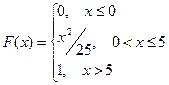
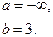
Д) 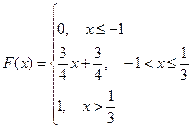
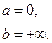
Е) 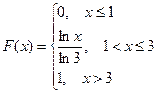
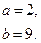
Ж) 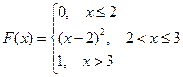
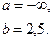
З) 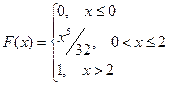
 2015-06-10
2015-06-10 1480
1480








