Выборочный метод. Статистические оценки параметров распределения

Генеральная совокупность это множество всех объектов, которые должны быть исследованы. Пусть для изучения количественного признака Х генеральной совокупности извлечена выборка 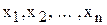объема n. Ранжированный ряд получается, если упорядочить выборку по возрастанию. Различные наблюдавшиеся значения 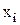признака Х называются вариантами, а числа, показывающие сколько раз каждая варианта встретилась в выборке – соответствующими им частотами 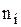(или относительными частотами 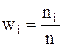). Последовательность вариант, записанная в порядке возрастания, с указанием их частот 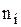(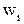), называется вариационным рядом.

Вариационный ряд называется дискретным, если выборка сделана из множества значений дискретной случайной величины Х, непрерывным, если выборка сделана из множества значений непрерывной случайной величины.

Общий вид дискретного вариационного ряда:

хi	x1	x2	…	xk
ni	n1	n2	…	nk

Здесь х_i – варианты, n_i – соответствующие им частоты.

Общий вид интервального вариационного ряда:

[аi;аi+1)	[a1;a2)	[a2;a3)	…	[ak;ak+1)
ni	n1	n2	…	nk

Здесь а_i – границы частичных интервалов. На которые разбивается выборка, n_i – соответствующие им частоты (количество выборочных данных, попавших в i-ый интервал.).

Эмпирической функцией распределения 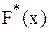называется функция, определяющая для каждого значения х относительную частоту события X<x, тo есть

,

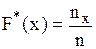где 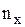- число вариант, меньших

Свойства функции :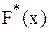

1. .

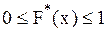2. 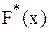– неубывающая функция, т.е. 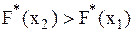, если .

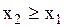3.Если 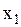– наименьшая варианта, то 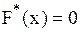, при .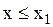

4.Если 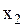– наибольшая варианта, то 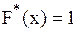, при .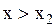

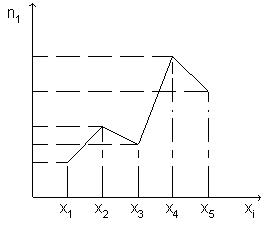
Полигоном частот называют, ломаную кривую, отрезки которой соединяют точки 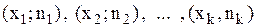. Пример полигона частот приведен на рисунках

Полигон Гистограмма

Полигоном относительных частот называют ломанную кривую, отрезки которой соединяют точки .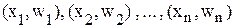

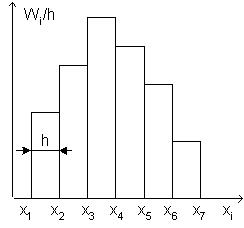
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению 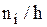(плотности частоты). Площадь гистограммы частот равна объему выборки n.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению 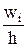(плотности относительной частоты). Площадь гистограммы относительных частот равна единице. Пример гистограммы относительных частот приведен на рис.2.

Пример. Найти эмпирическую функцию распределения 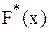по распределению выборки.

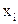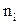Решение.

Воспользуемся формулой:

,

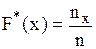где n – объем выборки (n=10+15+30+20+25=100),

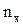– число вариант, меньших аргумента x. Так как 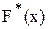является кусочно-постоянной (ступенчатой), разобьем область определения R на интервалы постоянства функции (см рисунок).

0 15 20 25 30 35

1. При x 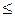15

вариант, меньших x в выборке нет, то есть 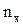= 0.

.

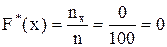2. При 15<x 20

варианты, меньшие x – это 10 вариант, каждая из которых равна 15, то есть 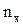=10. .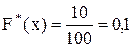

3. При 20<x 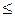25

вариант, меньших x – двадцать пять:

10 – равных 15 и 15 – равных 20, то есть 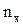=10+15=25. .

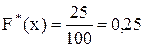4. При 25<x 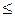30

вариант, меньших x – пятьдесят пять:

10 – равных 15, 15 – равных 20, 30 – равных 25, то есть 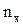=10+15+25=55.

.

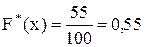5. При 30<x 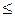35

вариант, меньших x – семьдесят пять:

10 – равных 15, 15 – равных 20, 30 – равных 25, 20 – равных 30, то есть 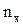=10+15+25+30=75. .

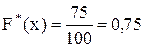6. При x>35

все 100 вариант меньше х. .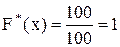

Таким образом, эмпирическая функция распределения имеет вид:

.

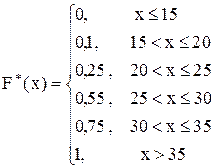Пусть θ_г – некоторый параметр генеральной совокупности, который невозможно вычислить. Но знать его значение (хотя бы приближенное, оценочное) надо. Поэтому по выборочным данным производят расчет статистических оценок данного генерального параметра.

Оценки параметров подразделяются на точечные и интервальные.

Точечной называется статистическая оценка генерального параметра θ_г, которая определяется одним числом θ_в

Интервальной называется оценка генерального параметра θ_г, которая

определяется двумя числами θ_в и θ_в- концами интервала, покрывающего оцениваемы генеральный параметр θ_г.

Для того, чтобы точечная оценка давала «хорошие» приближения оцениваемого параметра, она должна быть: несмещенной, эффективной, состоятельной.

Несмещенной называют такую точечную оценку θв, математическое ожидание которой равно оцениваемому генеральному параметру при любом объеме выборки, то есть M[θв ] = θг

Если равенство нарушается, то в этом случае оценки θ_в называется смещенной.

Эффективной называется точечная оценка θв, которая (при заданном объеме выборки) имеет наименьшую возможную дисперсию, то есть

M[(θв − θг)²] ⇒ min

Состоятельной называется точечная оценка θв, которая (с увеличением объема выборки) стремится по вероятности к оцениваемому параметру θг, то есть для любого достаточно малого δ > 0

lim P (θ − θ < δ)=1

N →∞

Несмещенной оценкой генеральной средней (генерального математического ожидания Mг [x]) служит выборочная средняя (выборочноематематическое ожидание):

Mв [x]= Σx_j⋅μ_j от j=1 до k

где x j, μj (j = 1, k) - данные из табл. 1.4. Кроме того, Mв [x] является состоятельной оценкой. Если случайная величина X подчинена нормальному закону распределения, то Mв [x] является и эффективной оценкой.

Смещенной оценкой генеральной дисперсии Dг [x] служит выборочная дисперсия:

D_в[Х ] =Σ (х_j- Mв [ х]²) μ_j от j=1 до k

Надежностью (доверительной вероятностью) оценки θв называется вероятность γ, с которой осуществляется событие θг − θв < δ, то есть

γ = P(θг − θв < δ). (1.8)

Обычно надежность оценки (доверительная вероятность γ) задается.

Причем в качестве γ берут число, близкое к единице (0,95; 0,99; 0,999).

Доверительным называется интервал, который с заданной надежностью γ покрывает оцениваемый генеральный параметр. В соотношении (1.8), если раскрыть модуль, получается P(− δ < θ_в − θ_г < δ) = γ или P(θ_в − δ < θ_г < θ_в + δ) = γ

Тогда интервал (θ_в − δ; θ_в+ δ); и есть доверительный интервал. Из общих соображений ясно, что длина доверительного интервала будет зависеть от объема выборки N и доверительной вероятности γ.

Построение доверительного интервала для генерального среднего

Пусть Х - случайная величина, имеющая нормальный закон распределения с параметрами μ, σ, т. е. X = N(μ, σ). Будем предполагать, что наблюдения над этой величиной независимы и проводятся в одинаковых условиях, т. е. возможные результаты X1, X2,..., Xn этих наблюдений обладают следующими свойствами:

X1, X2,..., Xn - независимые случайные величины;

закон распределения любой из величин X1, X2,..., Xn совпадает с законом распределения величины Х, т. е.

X1 = N(μ, σ), X2 = N(μ, σ),..., Xn = N(μ, σ).

Интервальная оценка математического ожидания нормального распределения при известной дисперсии

Как результат центральной предельной теоремы следующая Z-формула используется в данном случае

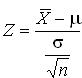
откуда имеем

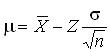
Так как выборочное среднее может быть больше или меньше, чем генеральный параметр, то предыдущее выражение берется в следующей форме:

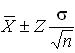
Отсюда получаем доверительный интервал в виде

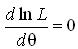
где α - уровень значимости, изображаемый площадью под кривой нормального распределения вне площади, соответствующей доверительной вероятности;

α/2 - площадь под кривой нормального распределения на правом и на левом хвостах распределения

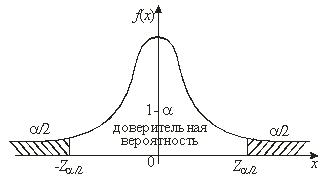
Уровень значимости используется, чтобы определить положение Z, значение которого определяется из таблицы функции Лапласа

Если мы хотим определить 95 %-й доверительный интервал для μ, то это означает, что из ста интервалов, построенных по случайным выборкам, взятым из генеральной совокупности, 95 интервалов будут накрывать генеральный параметр, а 5 интервалов - нет.

В данном случае формула в виде вероятностного утверждения имеет вид

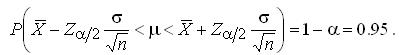
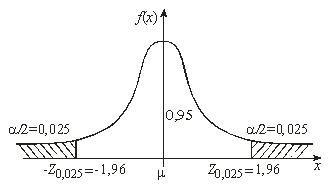
Откуда α = 0.05; α/2 = 0.025.

Распределение выборочного среднего для вероятности 0,95 имеет вид

Пример. Случайная величина Х распределена по N(μ, 1.1). По случайной выборке определено среднее арифметическое = 4.26, n=60. Определить 95 %-й доверительный интервал для μ и точность оценивания μ.

Решение

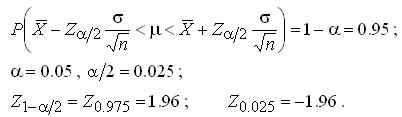
Доверительный интервал имеет вид

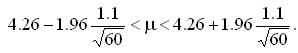
Точность оценивания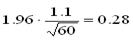

Окончательно имеем

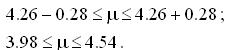
Примечание. Приводимая формула Z для выборочных средних может быть использована для выборок большого размера, несмотря на форму генерального распределения.

Эта же формула используется для выборок малого размера, если генеральная совокупность нормально распределена и генеральное σ известно.

Частость как точечная оценка вероятности события

Обозначим через р неизвестную вероятность появления случайного события А в единичном испытании.

Приближенное значение 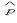вероятности р определяется в виде

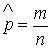
где - частость появления события А в n испытаниях;

m - число появления события А в n испытаниях.

Серия независимых испытаний, в каждом из которых событие А происходит с вероятностью q=1-p, является последовательностью испытаний Бернулли.

Теорема. Пусть m - число наступлений события А в n независимых испытаниях, р - вероятность наступления события А в каждом из испытаний. Тогда 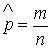- состоятельная, несмещенная и эффективная оценка вероятности р.