Пусть  и
и  — события, причем, событие
— события, причем, событие  наступает тогда, когда результатом испытания является один из элементарных исходов, входящих в
наступает тогда, когда результатом испытания является один из элементарных исходов, входящих в  , а событие
, а событие  наступает тогда, когда результатом испытания является один из элементарных исходов, входящих в
наступает тогда, когда результатом испытания является один из элементарных исходов, входящих в  .
.
Суммой или объединением 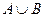 событий
событий  и
и  называется событие, состоящее в том, что произошло либо событие
называется событие, состоящее в том, что произошло либо событие  , либо
, либо  , либо оба события одновременно. На языке теории множеств
, либо оба события одновременно. На языке теории множеств 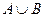 есть множество, содержащее как элементарные события, входящие в
есть множество, содержащее как элементарные события, входящие в  , так и элементарные события, входящие в
, так и элементарные события, входящие в  (рис. 1а).
(рис. 1а).
Произведением или пересечением 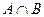 событий
событий  и
и  называется событие, состоящее в том, что произошли оба события
называется событие, состоящее в том, что произошли оба события  и
и  одновременно. То есть
одновременно. То есть 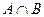 есть множество, содержащее элементарные исходы, входящие одновременно и в
есть множество, содержащее элементарные исходы, входящие одновременно и в  и в
и в  (рис. 1б).
(рис. 1б).
Разностью или дополнением 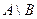 (читается «
(читается « без
без  ») события
») события  до
до  называется событие, состоящее в том, что произошло событие
называется событие, состоящее в том, что произошло событие  , но не произошло
, но не произошло  . То есть
. То есть 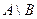 есть множество, содержащее элементарные исходы, входящие в
есть множество, содержащее элементарные исходы, входящие в  , но не входящие в
, но не входящие в  (рис. 1в).
(рис. 1в).
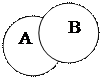 Рис. 1а
Рис. 1а
|
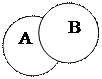 Рис. 1б
Рис. 1б
|
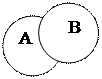 Рис. 1в
Рис. 1в
| 
Рис. 1г |
Рис. 1д |
Таким образом:
- события  и
и  несовместны, если
несовместны, если 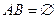 (рис. 1г);
(рис. 1г);
- событие  противоположно событию
противоположно событию 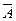 , если
, если 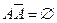 и
и 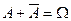 (рис. 1д);
(рис. 1д);
- события 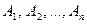 образуют полную группу событий, если
образуют полную группу событий, если 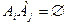 (
(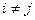 ) (события попарно несовместны) и
) (события попарно несовместны) и 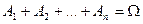 .
.
 2015-06-10
2015-06-10 666
666










