Необходимый объем выборки для некоторых способов формирования выборочной совокупности

Вид выборочного наблюдения	Повторный отбор	Бесповторный отбор
Собственно случайная выборка
а) при определении среднего размера признака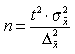
б) при определении доли признака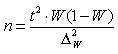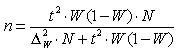
Механическая выборка	То же	То же
Типичная выборка:
а) при определении среднего размера признака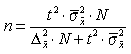
б) при определении доли признака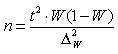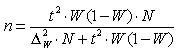
Серийная выборка:
а) при определении среднего размера признака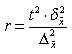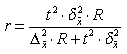
б) при определении доли признака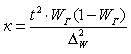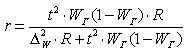

Напомним еще раз, что предельной ошибкой выборки принято считать максимально возможное расхождение 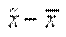, т.е. максимум ошибки при заданной вероятности ее появления.

В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше исследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы Чебышева—Ляпунова—Лапласа предельную величину ошибки простой случайной выборки для средней при достаточно большом объеме выборки (n) и повторном отборе можно определить по формуле:

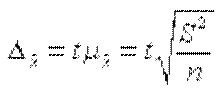, (8.10)

где 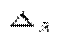— предельная ошибка, а t — коэффициент доверия из формулы (8.11) см. ниже. Фактически , где знаменатель дроби весьма близок к S ².

Из этой формулы средней ошибки простой случайной выборки видно, что величина ее зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше исследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:

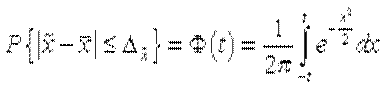, (8.11)

численные значения которой уже приводились в формуле (8.5).

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью. Вероятность появления ошибки, равной или большей утроенной средней ошибки выборки, т.е. Δ ≤ 3μ, крайне мала и равна 0,003 (1 - 0,997). Такие маловероятные события считаются практически невозможными, а потому величину Δ = 3μ можно принять за предел возможной ошибки выборки.

Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней Δ, которая показывает (с определенной вероятностью), насколько выборочная величина может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна (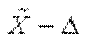), а верхняя граница — (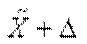), т.е. имеем:

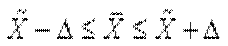. (8.12)

Интервал, в котором с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р — доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.

Вопросы для самопроверки:

· Что понимается под выборочным наблюдением?

· В чем состоит главная цель выборочного наблюдения?

· Как называется статистическая совокупность, из которой производится отбор единиц при организации выборочного наблюдения?

· Как называется абсолютная разница между средними, определенными по генеральной и выборочной совокупностям?

· Что означает коэффициент доверия в зависимости для определения предельной ошибки выборочного наблюдения?

· Виды формирования выборочной совокупности.

· Методы формирования выборочной совокупности.

· Способы отбора единиц при формировании выборочной совокупности.

· Что называется малой выборкой?

· Какой закон распределения используется в малых выборках?

· Почему при выборочном наблюдении неизбежны ошибки и как они классифицируются?

· Каковы условия правильного отбора единиц совокупности при выборочном наблюдении?

· Как производятся собственно случайный, механический, типический и серийный отборы?

· В чем различие повторной и бесповторной выборки?

· Что представляет собой средняя ошибка выборки (для средней и доли)?

· По каким расчетным формулам находят средние ошибки выборки (для средней и доли) при повторном и бесповторных отборах?

· Что характеризует предельная ошибка выборки и по каким формулам она исчисляется (для средней и доли)?

· Что показывает коэффициент доверия?

· В чем значение теоремы Чебышева—Ляпунова для решения задач выборочного наблюдения?

· Какими способами осуществляется распространение результатов выборочного наблюдения на всю совокупность?

· Зачем и как исчисляются предельные статистические ошибки выборки (для средней и доли)?

· По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью заданную точность наблюдения?