Говорят, что СВ  имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 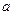 и
и 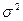 , где
, где 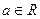 ,
, 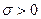 , и пишут
, и пишут 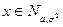 , если
, если  имеет следующую плотность распределения:
имеет следующую плотность распределения:
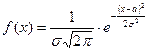 .
.
Нормальное распределение (НР), иначе называемое гауссовским по имени Карла Гаусса (Karl Fridrich Gauss), играет исключительно важную роль в теории вероятностей, т. к. он является предельным законом, к которому приближаются все другие законы распределения. Нормальный закон распределения проявляется в тех случаях, когда СВ  является результатом действия большого числа различных факторов, причем каждый фактор в отдельности на величину
является результатом действия большого числа различных факторов, причем каждый фактор в отдельности на величину  влияет незначительно и нельзя указать, какой именно в большей степени, чем остальные. Например, отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров, ошибки при измерении, отклонения при стрельбе и другие.
влияет незначительно и нельзя указать, какой именно в большей степени, чем остальные. Например, отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров, ошибки при измерении, отклонения при стрельбе и другие.
ФР СВ, имеющей НР, имеет вид:
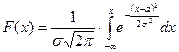 .
.
Нормальное распределение задается, как мы видим, с помощью плотности распределения. Связано это с тем, что нельзя выписать первообразную от функции 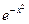 иначе как в виде интеграла, поэтому функцию распределения этого закона можно записать лишь в таком виде.
иначе как в виде интеграла, поэтому функцию распределения этого закона можно записать лишь в таком виде.
Как видно из формулы, нормальное распределение определяется двумя параметрами:
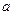 - математическое ожидание нормального распределения
- математическое ожидание нормального распределения 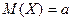 ;
;
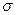 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Мы часто будем использовать обозначение 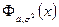 для функции распределения нормального распределения с параметрами
для функции распределения нормального распределения с параметрами 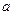 и
и 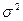 .
.
График плотности нормального распределения – нормальная кривая (кривая Гаусса)
Изменение величины параметра 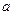 не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси
не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси 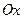 : вправо, если
: вправо, если 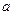 возрастает; влево, если
возрастает; влево, если 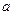 убывает.
убывает.
С возрастанием 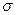 максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси 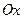 ; при убывании
; при убывании 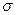 нормальная кривая становится более вытянутой в положительном направлении оси
нормальная кривая становится более вытянутой в положительном направлении оси 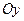 .
.
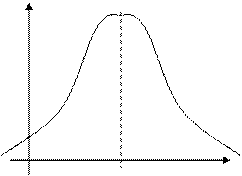
Но площадь, ограниченная нормальной кривой и осью 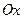 , остается равной единице.
, остается равной единице.
 2015-06-10
2015-06-10 351
351








