Нормальное распределение 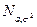 при
при 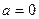 и
и 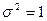 называется стандартным нормальным распределением.
называется стандартным нормальным распределением.
Плотность стандартного нормального распределения имеет вид 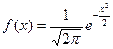 при любом
при любом 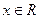 , а функция распределения
, а функция распределения
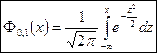 (1)
(1)
табулирована почти во всех математических справочниках. Функция (1) называется функцией Лапласа. Будем обозначать функцию Лапласа через 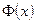 .
.
Установим связь между 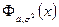 и
и 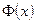 .
.
Свойство. Для любого 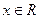 справедливо соотношение
справедливо соотношение
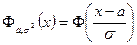 .
.
► 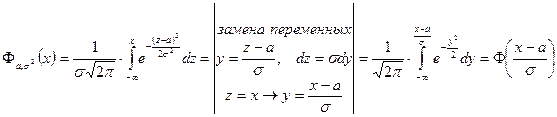 ◄
◄
Следствие. Если 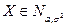 , то
, то
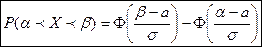 (2)
(2)
► Как известно, если СВ  задана плотностью распределения
задана плотностью распределения  , то вероятность того, что
, то вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  , такова:
, такова:
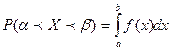 .
.
Для СВ  распределенной по нормальному закону:
распределенной по нормальному закону:
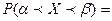
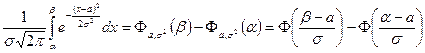 . ◄
. ◄
Отметим один важный частный случай формулы (2):
Найдем вероятность того, что отклонение нормально распределенной СВ  от ее математического ожидания по абсолютной величине меньше некоторого числа
от ее математического ожидания по абсолютной величине меньше некоторого числа 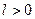 , т.е требуется найти вероятность осуществления неравенства
, т.е требуется найти вероятность осуществления неравенства 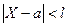 .
.
Произведем преобразования: 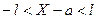 ,
, 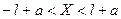 ,
,
По формуле (2):
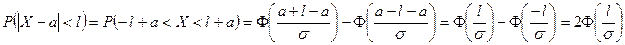 .
.
Т.е.
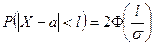 (3)
(3)
Таким образом, как мы видим, вычисление любых вероятностей для нормально распределенной случайной величины сводится к вычислению функции Лапласа 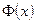 .
.
Свойства функции Лапласа.
1. 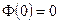 . ► Это следует из того, что при
. ► Это следует из того, что при 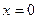 пределы интеграла (1) совпадают. ◄
пределы интеграла (1) совпадают. ◄
2. 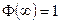 . ►
. ► 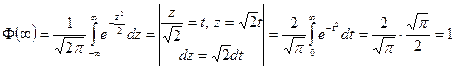 . Использовали интеграл Пуассона
. Использовали интеграл Пуассона 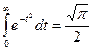 . ◄
. ◄
3. 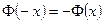 . ►
. ► 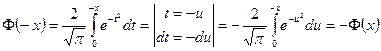 . ◄
. ◄
 График функции Лапласа:
График функции Лапласа: 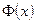
 | ||||
 | ||||
 |
Например: СВ  распределена по нормальному закону. МО и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что
распределена по нормальному закону. МО и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 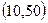 .
.
§ Воспользуемся формулой (12). По условию 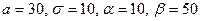 ,
,
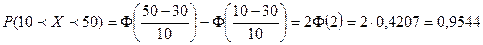 . §
. §
 2015-06-10
2015-06-10 376
376








