Зависимые и независимые СВ

Опр. СВ и 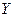называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины называются зависимыми.

Т-ма. ( Признак независимости СВ). Для того, чтобы НСВ и 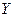были независимы, необходимо и достаточно, чтобы ПР системы 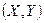была равна произведению плотностей распределения составляющих:

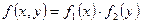. (9)