Совместное рассмотрение двух или нескольких СВ приводит к системе СВ (ССВ).
Опр. Законом распределения ССВ называется соотношение, устанавливающее связь между областями возможных значений ССВ и вероятностями появления системы в этих областях.
Рассмотрим систему двух СВ (СДСВ). Пусть  и
и 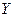 - ДСВ, возможные значения которых
- ДСВ, возможные значения которых 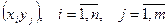 . Тогда распределение системы таких СВ может быть охарактеризовано указанием вероятностей
. Тогда распределение системы таких СВ может быть охарактеризовано указанием вероятностей 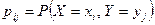 того, что СВ
того, что СВ  примет значение
примет значение 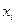 и одновременно с этим СВ
и одновременно с этим СВ 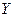 примет значение
примет значение 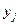 . Вероятности
. Вероятности 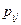 сводятся в таблицу вида
сводятся в таблицу вида
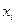
| 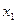
| 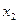
| … | 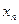
|
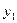
| 
| 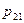
| … | 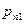
|
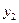
| 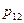
| 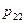
| … | 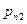
|
| … | … | … | … | |
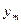
| 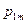
| 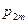
| … | 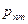
|
Все возможные события 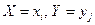 составляют полную группу несовместных событий, поэтому
составляют полную группу несовместных событий, поэтому 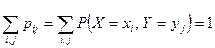 .
.
При этом
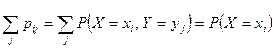 ;
;
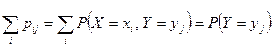 .
.
Опр. Функцией распределения СДСВ называется функция двух аргументов 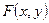 , равная вероятности совместного выполнения двух неравенств
, равная вероятности совместного выполнения двух неравенств 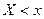 и
и 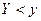 , т.е.
, т.е.
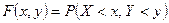 (1)
(1)
Геометрически ФР СДСВ представляет собой вероятность попадания случайной точки 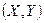 в левый нижний бесконечный квадрант плоскости с вершиной в точке
в левый нижний бесконечный квадрант плоскости с вершиной в точке 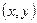 :
:
 |
Такая геометрическая интерпретация позволяет наглядно иллюстрировать следующие свойства ФР СДСВ:
1. Если один из аргументов стремится к 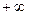 , то ФР системы стремится к ФР одной СВ, соответствующей другому аргументу, т.е.
, то ФР системы стремится к ФР одной СВ, соответствующей другому аргументу, т.е.
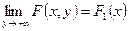 ;
; 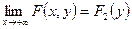 . (рис. 1б и в)
. (рис. 1б и в)
►Отодвигая одну из границ квадранта в 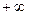 , квадрант превращается в полуплоскость. Вероятность же попадания случайной точки в такую полуплоскость есть функция распределения одной из величин, входящих в систему. ◄
, квадрант превращается в полуплоскость. Вероятность же попадания случайной точки в такую полуплоскость есть функция распределения одной из величин, входящих в систему. ◄
2. Если оба аргумента стремятся к 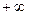 , то ФР системы стремится к единице, т.е.
, то ФР системы стремится к единице, т.е.
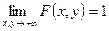 .
.
► Попадание во всю плоскость есть достоверное событие.◄
3. При стремлении одного или обоих аргументов к 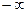 ФР стремится к нулю, т.е.
ФР стремится к нулю, т.е.
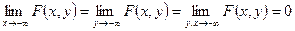 .
.
4. ФР является неубывающей функцией по каждому аргументу, т.е
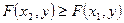 , если
, если 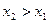 ;
;
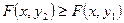 , если
, если 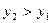 .
.
5. При 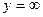 ФР системы становится ФР составляющей
ФР системы становится ФР составляющей  :
:
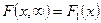 ,
,
а при 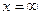 ФР системы становится ФР составляющей
ФР системы становится ФР составляющей 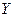 :
:
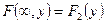 .
.
6. Вероятность попадания случайной точки 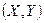 в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле
в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле
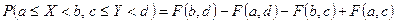 . (2)
. (2)
Опр. Плотностью распределения системы непрерывных СВ называется функция
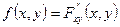 (3)
(3)
Из (1) и (3) следует, что ФР 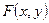 есть вероятность попадания в квадрант, ограниченный абсциссами
есть вероятность попадания в квадрант, ограниченный абсциссами 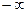 ,
,  и ординатами
и ординатами 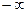 ,
, 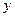 , поэтому
, поэтому
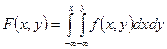 (4)
(4)
Свойства плотности распределения СДСВ.
1. ПР есть функция неотрицательная, т.е. 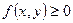 .
.
2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице:
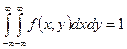 .
.
 2015-06-10
2015-06-10 559
559








