Наивероятнейшее число появления событий в последовательности независимых испытаний

Опр.: Наивероятнейшим числом m₀ наступления соб. А в n независим. испытаниях назыв. число, для кот. вер. 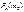превышает или по крайней мере не менее вер. каждого из остальных возм. исходов исп. Пусть соб. А наступило m₀ раз в n испы. Вер. появл. соб. А обозначим p; P(A)=p, а 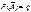, тогда по формуле Бернули 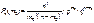. По определению: 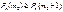-формула (1); 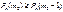-формула (2). Из нер-ва (1) получаем: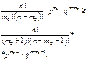 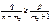; ; 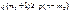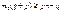. Т.к. q+p=1, то 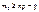. Из нер-ва (2) получаем: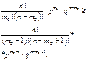 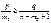; ; 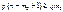; 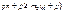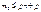. Т,о. для нахождения наивероятнейшего числа мы получили нер-во: 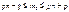. Замечание 1: Длина интервала, определяемая нер-вом равна 1; Замечание 2: Если границы интервала – дробные числа, то значение наивероятнейшего числа одно. Если границы – целые числа, то знач. наивер. числа два.