Плотность распр. вер. непрерывной СВ и ее св-ва

Ф-ция распр. вер-тей непрерывной СВ (НСВ) дает полную вер-ную хар-ку ее поведения. Однако задание НСВ с пом. ф-ции распр. не является единственным. Ее можно задать с пом. др. ф-ции, кот. называется дифференциальной ф-цией распр. или плотностью распр. вер-тей. Пусть X – НСВ с интегральной ф-цией распр. F(x). F(x) непрерывна и дифференцируема в исследуемом интервале. Рассмотрим вер. попадания знач. СВ в интервал (x; x+Dx). P(x<X<x+Dx) = F(x+Dx) – F(x), т.е. вер. равна приращению ф-ции на этом участке. Определим теперь вер., кот. приходится на единицу длины рассматриваемого участка. Для этого разделим обе части последнего рав-ва на Dx: 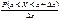= 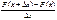Перейдем к пределу 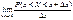= 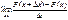; лев часть равна = 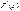; 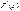= f(x). Опр.: Дифференц. ф-цией распр. или плотностью распр. вер. называется 1-ая производная от интегральной ф-ции распр. Замечание: Для хар-ки распр. вер. ДСВ дифференц. ф-ция распр. неприменима. Основные св-ва дифференц. ф-ции распр.: 1) Для 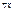f(x) неотрицательна, т.е. f(x) 0. Док-во: Следует из определения ф-ции плотности F(x) – неубыв. ф-ция, значит ее производная неотрицательна, т.е. F’(x) = f(x) 0; 2) Для дифференциальной ф-ции распр. имеет место равенство P(a<X<b) = 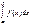. Док-во: Т.к. ф-ция F(x) явл. первообразной для функц. f(x), то из формулы (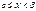) = F(b)-F(a) и формулы Ньютона-Лейбница вытекает вер. того, что P(a<X<b) = F(b)-F(a) = 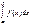; 3)Для дифференц. ф-ции распр. имеет место рав-во: 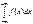=1. Док-во: Согласно опр. несобств. интеграла по бескон. пределам и 3-му св-ву ф-ции распр. имеем 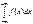= 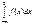+ 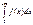= 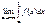+ 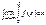= 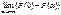+ 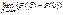= 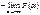+ 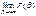=0+1=1; 4) Для интегр. и дифференц. ф-ции распр. имеет место рав-во: F(x) = 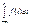. Док-во: 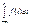= = 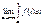= 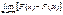F(x) - 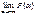= F(x)-0=F(x). Замечание: Если СВ Х принимает значение только в некот. интервале (a,b), то 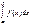=1.