Вер. попадания СВ в заданный интервал

Вер. попадания СВ Х в задан. интервал [a,b)

равна приращению ее ф-ции распр. на этом интервале, т.е. вер. того, что P(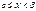)= F(b) - F(a). Эта формула следует из формулы F(х₂)=F(х₁)+ P(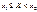) – вопрос №24, если вместо точек х₁, ₂ взять точки a и b. Cв-во: Вер. любого отдельного знач. НСВ равна 0. Док-во: Воспользуемся рав-вом P(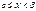)= F(b) - F(a) и устремим b к a. (b®a). Тогда получим 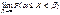= 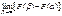. В левой части посл. рав-ва в пределе вместо вер. попадания знач. СВ в интервал [a,b) получим вер. того, что СВ приняла отдельно взятое значение a, т.е. P(X=a). Значение предела в правой части рав-ва зависит от того, явл. ли ф-ция F(x) непрерывной в точке a или имеет в ней разрыв. Если ф-ция имеет разрыв, то предел равен величине скачка ф-ции F(x) в точке a. Т.к. по предположению ф-ция F(x) всюду непрерывна, то 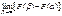= F(a) - F(a) = 0. Т.о. 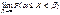= = 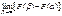P(X=a)=0. При непрерывн. распр. вер-тей, т.е. когда ф-ция распр. непрерывна, вер. попадания знач. НСВ на сколь угодно малый участок отлична от 0, тогда как вер. попадания в строго опр. точку равна 0. Воспользовавшись последним св-вом, докажем, что для НСВ выполняются след. рав-ва: Р(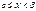) = = 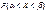= 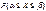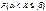. Докажем одно из соотношений. Соб. 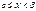представл. собой сумму 2-ух несовместн. соб. X=a и 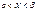. Тогда по теор. слож. вер. имеем Р(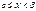) = P(X=a) + 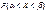. Согласно посл. св-ву P(X=a)=0, тогда P(X=a) + 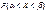= = 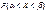F(b) - F(a). Сл-но 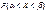= F(b) - F(a).