Начальным моментом к-того порядка СВ Х называется мат. ожидание(м.о.) к-той степени этой вел-ны. Начальн. момент обозначается 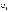 = M(X)k. Центральным моментом к-того порядка СВ Х назыв. м.о. к-той степени отклонения СВ Х от ее м.о., т.е.
= M(X)k. Центральным моментом к-того порядка СВ Х назыв. м.о. к-той степени отклонения СВ Х от ее м.о., т.е. 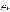 = (X – M(X))k. Для ДСВ и НСВ формулы для вычисления моментов приведены в таблице:
= (X – M(X))k. Для ДСВ и НСВ формулы для вычисления моментов приведены в таблице:
| Моменты | ДСВ | НСВ |
| Начальный | 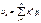 | 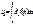 , где f(x) – ф-ция плотности распр. , где f(x) – ф-ция плотности распр. |
| Цент Ральн. | 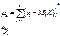 | 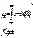 |
При к=1 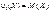 ; при к=2
; при к=2 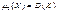 . Центр. моменты
. Центр. моменты 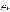 могут быть выражены через нач. моменты
могут быть выражены через нач. моменты 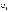 по формулам:
по формулам: 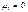 ;;
;; 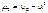
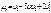 . м.о. или нач. момент 1-го порядка хар-ет ср. значение СВ.
. м.о. или нач. момент 1-го порядка хар-ет ср. значение СВ. 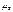 или дисперсия хар-ет степень рассеивания распр. СВ Х отн-но м.о. M(X).
или дисперсия хар-ет степень рассеивания распр. СВ Х отн-но м.о. M(X). 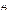 служит для хар-ки ассиметрии или скошенности распр. Он имеет размерность куба СВ. Чтобы получить безразмерную вел-ну, ее делят на
служит для хар-ки ассиметрии или скошенности распр. Он имеет размерность куба СВ. Чтобы получить безразмерную вел-ну, ее делят на 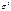 , где d - среднеквадратич. отклонение. Коэфф ассиметрии
, где d - среднеквадратич. отклонение. Коэфф ассиметрии 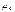 служит для хар-ки крутости, т.е. островершинности или плосковершинности распр. Эти св-ва описываются с помощью эксцесса.
служит для хар-ки крутости, т.е. островершинности или плосковершинности распр. Эти св-ва описываются с помощью эксцесса.
31. Биномиальный закон распределения.
Пусть проводится n независим. испытаний, в кажд. из которых соб. А может появиться, либо не появиться. Вер. появл. соб. А в единичном испытании постоянна и не меняется от исп. к исп.. Рассмотрим в кач-ве ДСВ Х число появлений соб. А в этих исп. Формула, позволяющая найти вер. появления m раз соб. А в n испытаниях – это форм. Бернулли. Опр.: ДСВ Х, кот. может принимать только целые неотриц. знач. с вер. Pn(m)=P(X=m)= 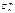 pmqn-m, где p+q=1, p>0, q>0, m=
pmqn-m, где p+q=1, p>0, q>0, m= 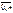 называется распределенной по биномиальному закону, а p – параметром биномиальн. распр. Ряд распр. ДСВ Х распределенной по биномиальному закону можно представить в виде:
называется распределенной по биномиальному закону, а p – параметром биномиальн. распр. Ряд распр. ДСВ Х распределенной по биномиальному закону можно представить в виде:
| X | K | n | ||
| p | 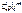 | 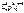 | 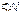 |
Ф-ция 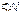 распр. в этом случае опр-ся формулой F(x)=
распр. в этом случае опр-ся формулой F(x)= 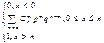 . Найдем числовые хар-ки этого распр.. M(X) =
. Найдем числовые хар-ки этого распр.. M(X) = 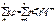 (рав-во 1). Запишем рав-во, являющееся биномом Ньютона: (p+q)n=
(рав-во 1). Запишем рав-во, являющееся биномом Ньютона: (p+q)n= 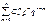 . Продифференцируем последнее рав-во по p: n(p+q)n-1=
. Продифференцируем последнее рав-во по p: n(p+q)n-1= 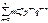 . Умножим последнее рав-во на p: np(p+q)n-1=
. Умножим последнее рав-во на p: np(p+q)n-1= 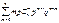 . Сравнивая получен. рав-во с рав-вом (1), получаем, что np(p+q)n-1 = M(X). Т.к. p+q=1, то M(X)= np. Для вычисления дисперсии ДСВ, распределенной по биномиальному закону, воспольз. формулой D(X)= M(X2) – (M(X))2. Для СВ распределенной по биномиальн. закону: M(X2) =
. Сравнивая получен. рав-во с рав-вом (1), получаем, что np(p+q)n-1 = M(X). Т.к. p+q=1, то M(X)= np. Для вычисления дисперсии ДСВ, распределенной по биномиальному закону, воспольз. формулой D(X)= M(X2) – (M(X))2. Для СВ распределенной по биномиальн. закону: M(X2) = 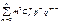 . Продифференцируем рав-во (p+q)n =
. Продифференцируем рав-во (p+q)n = 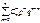 дважды по p. Получим n(n–1)(p+q)n—2=
дважды по p. Получим n(n–1)(p+q)n—2= 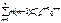 . Умножим последнее рав-во на p2 и преобразуем правую часть рав-ва: n(n – 1)(p+q)n —2 p2=
. Умножим последнее рав-во на p2 и преобразуем правую часть рав-ва: n(n – 1)(p+q)n —2 p2= 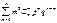 —
— 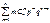 ; n2p2 – np2 = M(X2) —
; n2p2 – np2 = M(X2) — 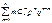 ; n2p2 – np2 = M(X2) – M(X). Для ДСВ распределенной по биномиальн. закону M(X)= np, т.е. n2p2 – np2 = M(X2) – np; M(X2)= n2p2 – np2 + np; D(X)= n2p2 – np2 + np — n2p2 = np(1 – p) = npq. Значит дисперсия ДСВ распределенной по биномиальн. закону вычисляется по формуле: D(X) = npq.
; n2p2 – np2 = M(X2) – M(X). Для ДСВ распределенной по биномиальн. закону M(X)= np, т.е. n2p2 – np2 = M(X2) – np; M(X2)= n2p2 – np2 + np; D(X)= n2p2 – np2 + np — n2p2 = np(1 – p) = npq. Значит дисперсия ДСВ распределенной по биномиальн. закону вычисляется по формуле: D(X) = npq. 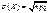 .
.
 2015-06-10
2015-06-10 1037
1037








