Отдел технического контроля проверил 200 партий одинаковых изделий и получил следующее эмпирическое распределение, частота ni – количество партий, содержащих xi нестандартных изделий.требуется при уровне значимости 0,05 проверить гипотезу о том, что число нестандартных изделий Х распределено по закону Пуассона.
| xi | |||||
| ni |
Решение.
Найдем выборочную среднюю:
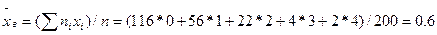
Примем в качестве оценки параметра l распределения Пуассона выборочную среднюю l=0,6. Следовательно, предполагаемый закон Пуассона 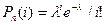 имеет вид
имеет вид 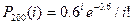 .
.
Положив i=0,1,2,3,4 найдем вероятности Piпоявления i нестандартных изделий в 200 партиях: 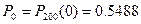 ,
, 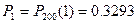 ,
, 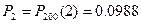 ,
, 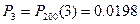 ,
, 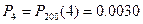 .
.
Найдем теоретические частоты по формуле 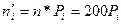 . Подставив в эту формулу значения вероятности, получим
. Подставив в эту формулу значения вероятности, получим 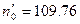 ,
, 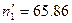 ,
, 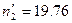 ,
, 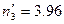 ,
, 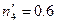 .
.
Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого составим расчетную таблицу. Объединим малочисленные частоты(4+2=6) и соответствующие им теоретические частоты (3,96+0,6=4,56).
| i | ni | 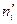 | ni- 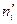 | (ni- 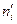 )2 )2 | (ni- 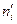 )2/ )2/ 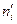 |
| 109.76 | 6.24 | 38.9376 | 0.3548 | ||
| 65.86 | -9.86 | 97.2196 | 1.4762 | ||
| 19.76 | 2.24 | 5.0176 | 0.2539 | ||
| 4.56 | 1.44 | 2.0736 | 0.4547 | ||
| å | 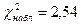 |
 2015-06-10
2015-06-10 753
753








