2015-06-10
2301
Заданы математическое ожидание а=3 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х.
- Написать плотность распределения вероятностей и схематично построить ее график.
- Найти вероятность того, что х примет значение из интервала (2;10).
- Найти вероятность того, что х примет значение превышающее 10.
- Найти интервал симметричный относительно математическое ожидание, в котором с вероятностью g=0,95 будут заключены значения величины х.
Решение.
1). Составим функцию плотности распределения случайной величины Х с параметрами а=3, s=5 воспользовавшись формулой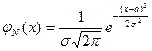 
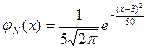. Построим схематически график функции 
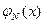. Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=3 и имеет max в этой точке, равный 
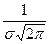, т.е. 
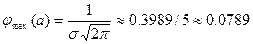и две точки перегиба 
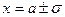с ординатой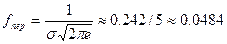 
Построим график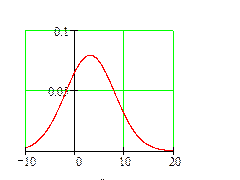 
2) Воспользуемся формулой: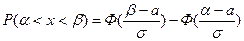 
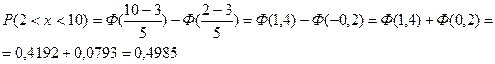
Значения функций найдены по таблице приложений.
3) 
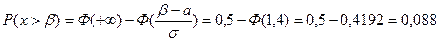
4) Воспользуемся формулой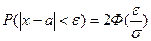 
. По условию вероятность попадания в интервал симметричный относительно математического ожидания 
. По таблице найдем t, при котором Ф(t)=0,475, t=2. значит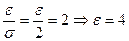 
. Таким образом, 
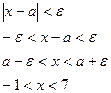. Ответ хÎ(-1;7).
|
|
|
