Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется:
1) найти плотность распределения вероятностей f(x);
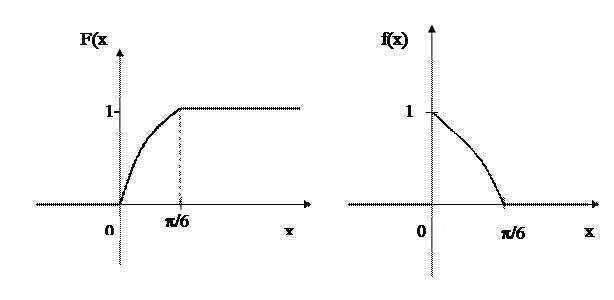
2) схематично построить графики функций f(x) и F(х);
3) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х;
4) найти вероятность того, что Х примет значение из интервала (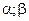 ).
).
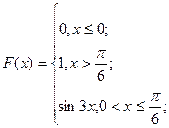
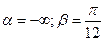
Решение.
1) плотность распределения случайной величины равна первой производной от функции распределения.
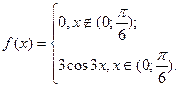
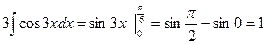 . Условие нормировки выполнено.
. Условие нормировки выполнено.
2) 
3) Для нахождения математического ожидания используем формулу 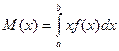 , где a,b начало и конец интервала, где определена плотность.
, где a,b начало и конец интервала, где определена плотность.
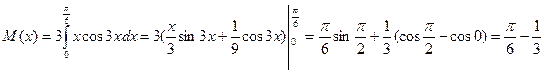 ;
;
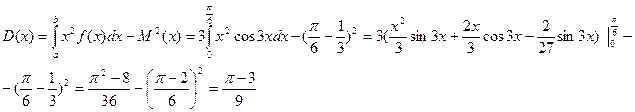
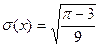
4) 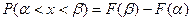
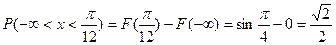 .
.
Приложение. Для вычисления интегралов используем формулы.
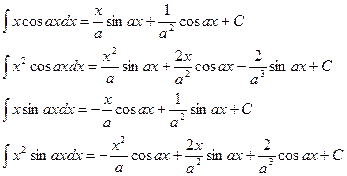
 2015-06-10
2015-06-10 531
531








