Числовые характеристики системы двух случайных величин

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, такие как корреляционный момент и коэффициент корреляции.

Корреляционный момент

Характеристикой зависимости между случайными величинам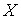и и 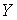служит математическое ожидание произведения отклонени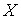й и 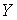от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:

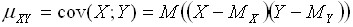
Для вычисления корреляционного момента дискретных величин используют формулу:

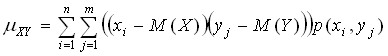
а для непрерывных величин – формулу:

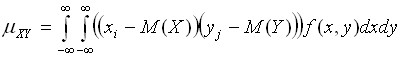
Эту формулу можно интерпретировать так. Если при больших значениях более вероятны большие значения, а при малых значениях 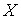более вероятны малые значения 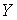, то в правой части формулы положительные слагаемые доминируют, и ковариация принимает положительные значения.

Если же более вероятны произведения 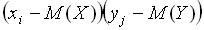, состоящие из сомножителей разного знака, то есть исходы случайного эксперимента, приводящие к большим значениям в основном приводят к малым значениям и наоборот, то ковариация принимает большие по модулю отрицательные значения.

В первом случае принято говорить о прямой связи: с ростом 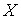случайная величина 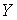имеет тенденцию к возрастанию.

Во втором случае говорят об обратной связи: с ростом 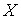случайная величина 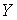имеет тенденцию к уменьшению или падению.

Если примерно одинаковый вклад в сумму дают и положительные и отрицательные произведения 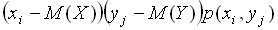, то можно сказать, что в сумме они будут “гасить” друг друга и ковариация будет близка к нулю. В этом случае не просматривается зависимость одной случайной величины от другой.

Теорема. Корреляционный момент двух независимых случайных величин 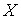и 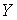равен нулю.

Доказательство. Так как 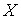и 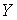– независимые случайные величины, то их отклонения 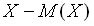и 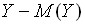также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим:

.

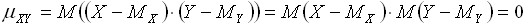Ковариацию можно представить в виде:

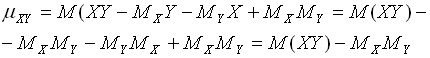
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин 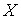и 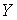. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным.