2015-06-10
1596
ФБГОУ ВПО
“ВоронежскИЙ государственнЫЙ УНИВЕРСИТЕТ ИНЖЕНЕРНЫХ технологиЙ”
Кафедра информационных технологий,
Моделирования и управления
ТЕОРИЯ МНОЖЕСТВ
Методические указания к практическим и лабораторным занятиям
по дисциплине "Дискретная математика"
Для бакалавров, обучающихся
По направлениям 230400, 230700
И специалистов – по специальности 090303
Очной формы обучения
Метод математической индукции
Метод математической индукции – универсальный способ доказательства утверждений, зависящих от натурального аргумента n. Он основан на следующем принципе математической индукции: утверждение справедливо для любого натурального n, если: 10 оно справедливо для n = 1;
20 из того, что оно верно для всех n £ k (k ³ 1) следует его справедливость для n = k + 1.
Этот принцип, являющийся одной из аксиом натурального ряда можно перефразировать так: если в цепочке утверждений Р(n) первое утверждение Р(1) верно, а из справедливости Р(k) следует справедливость Р(k + 1), то вся цепочка состоит из верных утверждений.
|
|
|
Задача 1. Найти сумму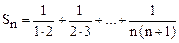 
.
Решение. Имеем: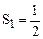 
; 
; 
; 
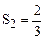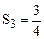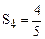. Есть подозрение, что 
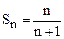. Докажем эту формулу.
10. При n = 1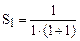 
– формула верна.
20. Предположим, что для произвольного k ³1 для всех n£ k 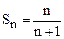. В частности, для n = k 
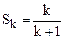. Найдем 
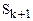. Имеем 
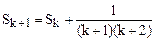. По предположению это равно
= 
= 
= 
,
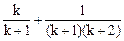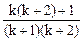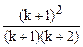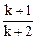что и требовалось доказать.
Слово “индукция” переводится как “наведение”. Во многих отраслях науки используют метод простой (не математической) индукции – вывод, полученный после рассмотрения ряда частных случаев (согласно принципу простой индукции – от частного к общему). В основном так поступают, обобщая результаты каких-то экспериментов. Так, в предыдущем примере, при выводе возможной формулы для Sn, предварительно были найдены значения S1, S2, S3, …. Однако индуктивное утверждение может быть неверным, простая индукция позволяет лишь выдвинуть гипотезу, которую надо доказать, например, с помощью математической (полной) индукции. Можно привести много примеров, когда простая ндук-ция приводит к ошибочным выводам. Например, анализируя числа 1, 3, 5, 7 можно прийти к неверноиу заключению, что все не-четные числа являются простыми.
Слово ”индукция” в названии рассматриваемого метода, видимо, связано с тем, что для его использования необходимо сначала догадаться, что именно следует доказать, т.е. выдвинуть гипотезу. Обычно это делается с помощью простой индукции.
Задача 2. “Докажем”, что все натуральные числа равны между собой. Предположим, что k = k + 1. Прибавим по 1 к обеим частям этого равенства. Получим k + 1 = k + 2, что и требовалось доказать. Ошибка этого “доказательства” состоит в отсутствии проверки утверждения при n = 1.
|
|
|
Задача 3. Доказать неравенство 2n > 2n + 1 при n ³ 3.
Решение.
10. 23 > 7.
20. 2k + 1 = 2×2k > 2(2k + 1) = 4k + 2 = (2k + 3) + (2k – 1) > 2k + 3.
Задача 4. Доказать, что для любого n ³ 0 число 11n + 2 + 122n + 1 делится на 133.
Решение.
10. 112 + 121 = 133 – верно при n = 0.
20. 11k +3 + 122(k + 1) +1 = 11×11k + 2 + 144×122k + 1 = (144–133) ´ ´11k + 2 + 144×122k + 1 = 144 × (11k + 2 + 122k + 1) – – 133×11k + 2.
В полученной разности уменьшаемое делится на 133 по предположению, а вычитаемое содержит множитель 133. Следовательно, все выражение делится на 133.
