Число P (A), поставленное в соответствие каждому наблюдаемому в опыте событию A и удовлетворяющее аксиомам
1) 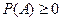 ;
;
2) P (W)=1;
3) Для любой последовательности A 1,…, An,…попарно несовместных событий (AiAj =Æ при i ¹ j):
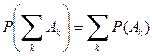
называется вероятностью события А. В частном случае, для пространства W={ w 1,…, wn } с равновероятными исходами 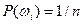 , получаем классическое определение вероятности.
, получаем классическое определение вероятности.
Пример.
В урне имеются 4 шара с номерами 1, 2, 3, 4. Из урны извлекают два шара. Найти вероятность события А – сумма номеров извлеченных шаров равна 5.
Решение.
Построим пространство элементарных событий W для заданного в условии испытания. Оно состоит из шести элементарных событий: 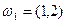 ,
, 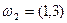 ,
, 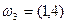 ,
, 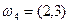 ,
, 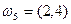 ,
, 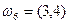 . Все перечисленные события равновозможны, поэтому
. Все перечисленные события равновозможны, поэтому
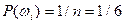 .
.
Далее, событие А – сумма номеров на извлекаемых из урны шарах должна быть равна 5, состоит из событий 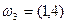 и
и 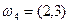 , т.е.
, т.е. 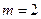 . Отсюда
. Отсюда
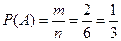 .
.
Геометрическое определение вероятности. Если событие А ‑ попадание в область G точки, наудачу выбранной в области W, то вероятность события A определяется формулой
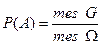 ,
,
где mes G - мера области g (длина, площадь, объем), mes W - мера области W (длина, площадь, объем).
Пример.
В круг вписан квадрат. Найти вероятность события А – точка, брошенная наудачу внутрь круга, окажется внутри квадрата.
Решение.
Пространство W - множество точек круга (радиуса R). Количественной характеристикой (мерой) пространства W является площадь круга, а количественной характеристикой бесконечного множества случаев, благоприятствующих событию А, служит площадь квадрата. Поэтому
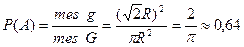 .
.
 2015-06-10
2015-06-10 641
641








