Закон распределения вероятностей. Случайная величина Х называется дискретной, если множество ее возможных значений конечно или счетно. Пусть ДСВ принимает значения 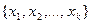 . Наблюдаемые события заключаются в том, что СВ Х принимают значение
. Наблюдаемые события заключаются в том, что СВ Х принимают значение 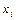 , тогда соответствующие вероятности
, тогда соответствующие вероятности 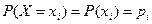 определяют закон распределения ДСВ Х. Его удобно представить в виде таблицы – ряда распределения СВ Х:
определяют закон распределения ДСВ Х. Его удобно представить в виде таблицы – ряда распределения СВ Х:
| Х | x 1 | x 2,… | xk | … |
| pi | p 1 | p 2,… | pk | … |
Отметим, что все 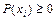 , кроме того,
, кроме того, 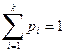 .
.
Графически ряд распределения изображается в виде многоугольника распределения. Для его построения возможные значения СВ откладываются по оси абсцисс, а соответствующие им вероятности по оси ординат. Полученные точки соединяются ломаной линией.
Для ДСВ Х функция распределения имеет вид
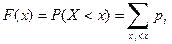 .
.
Числовые характеристики СВ. Математическим ожиданием ДСВ называется сумма
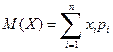 . (1)
. (1)
Свойства математического ожидания:
1) Математическое ожидание постоянной (неслучайной) величины
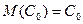 ;
;
2) При умножении СВ на постоянный множитель
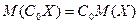 .
.
Числовой характеристикой рассеивания СВ относительно ее математического ожидания является дисперсия. Дисперсией СВ называется число
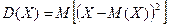 .
.
Для ДСВ получаем по определению (1):
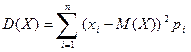 . (2)
. (2)
Основные свойства дисперсии:
1) 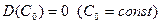 - дисперсия постоянной величины равна нулю;
- дисперсия постоянной величины равна нулю;
2) 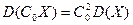 ;
;
3) 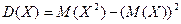 .
.
Средним квадратическим отклонением (СКО) СВ называется квадратный корень из дисперсии
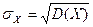 .
.
Пример.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение ДСВ, описываемой рядом распределения:
| xi | |||
| pi | 0,3 | 0,1 | 0,6 |
Решение.
Найдем математическое ожидание по формуле (1):
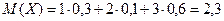 .
.
Найдем дисперсию по формуле (2):
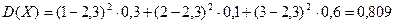 .
.
Отсюда получаем СКО:
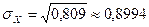 .
.
Биномиальный закон распределения. Рассмотрим серию из n независимых испытаний, т.е. таких опытов, в которых вероятность появления того или иного результата не зависит от того, какие результаты наступили или наступят в остальных испытаниях. В каждом из n однотипных опытов некоторое событие А может наступить с вероятностью р (или не наступить с вероятностью q =1- p). Данная схема испытаний называется схемой Бернулли. Вероятность того, что в серии из n независимых испытаний событие А появится ровно k раз (и не появится n – k раз), выражается формулой Бернулли
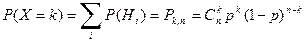 . (3)
. (3)
Закон распределения ДСВ X, равной количеству реализаций события A в серии из n независимых испытаний по схеме Бернулли, называется биномиальным.
Для ДСВ, распределенной по биномиальному закону с параметрами n (количество испытаний) и p (вероятность реализации события A при одном испытании):
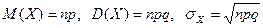 .
.
Пример.
Среди деталей, вырабатываемых рабочим, бывает в среднем 4% брака. Какова вероятность того, что среди взятых на испытание 6 изделий бракованных будет ровно 2?
Решение.
Вероятность брака 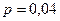 , тогда
, тогда 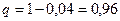 . По формуле Бернулли (3):
. По формуле Бернулли (3): 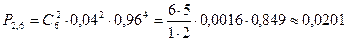 .
.
Пример.
Производится 4 независимых выстрела с вероятностью попадания в цель 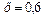 при каждом выстреле. Построить ряд распределения и многоугольник распределения числа попаданий в мишень. Построить график функции распределения для полученного ряда распределения.
при каждом выстреле. Построить ряд распределения и многоугольник распределения числа попаданий в мишень. Построить график функции распределения для полученного ряда распределения.
Решение.
Пусть х – число попаданий в мишень. Вероятные значения х есть 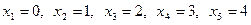 . Вероятности попаданий вычисляются по формуле Бернулли:
. Вероятности попаданий вычисляются по формуле Бернулли:
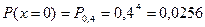 ;
;
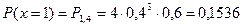 ;
;
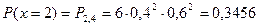 ;
;
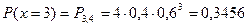 ;
;
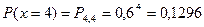 .
.
Ряд распределения имеет вид:
| xi | |||||
| pi | 0,0256 | 0,1536 | 0,3456 | 0,3456 | 0,1296 |
Построим многоугольник распределения:
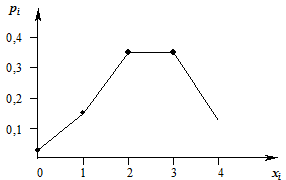
Найдем некоторые значения функции 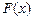 :
:
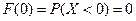 ;
;
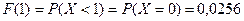 ;
;
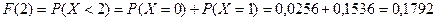 ;
;
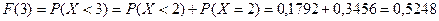 ;
;
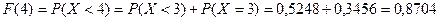 ;
;
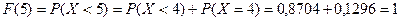 ;
;
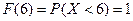 и т.д.
и т.д.
График функции распределения имеет вид:
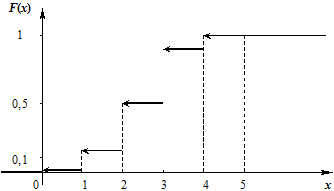
Закон распределения Пуассона. В практике инженерных расчетов встречаются задания, использующие схему испытаний Бернулли, для которой общее число опытов n, образующих серию, велико, а вероятность появления события А после одного испытания мала. В таких случаях применяется закон Пуассона:
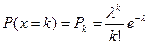 , (4)
, (4)
где 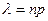 .
.
Для ДСВ, распределенной по закону Пуассона:
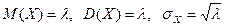 .
.
Пример.
Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Станция обслуживает 300 абонентов. Какова вероятность того, что в течение часа позвонят 4 абонента?
Решение.
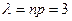 .
.
По формуле (4):
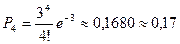 .
.
 2015-06-10
2015-06-10 1020
1020








