Закон распределения вероятностей. Случайная величина Х называется непрерывной, если существует такая функция 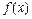 , называемая плотностью распределения вероятностей, что при всех
, называемая плотностью распределения вероятностей, что при всех 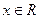
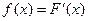 .
.
Плотность распределения вероятностей обладает свойствами:
1. 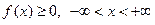 ;
;
2. 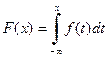 ;
;
3. 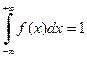 (условие нормировки);
(условие нормировки);
4. 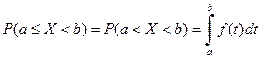 .
.
Числовые характеристики случайных величин. Для НСВ с функцией плотности распределения f (x) математическиможиданием называется интеграл
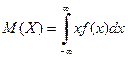 , (5)
, (5)
а дисперсией
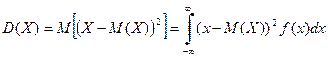 . (6)
. (6)
Свойства математического ожидания и дисперсии являются общими для НСВ и ДСВ и имеют тот же вид 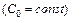 :
:
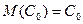 ,
, 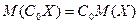 ,
, 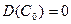 ,
, 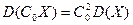 . Вновь
. Вновь 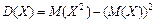 , а под СКО понимается
, а под СКО понимается 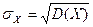 .
.
Равномерное распределение. НСВ Х называется распределенной равномерно на отрезке 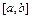 , если ее плотность распределения вероятностей:
, если ее плотность распределения вероятностей:
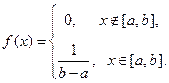
Пример.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение НСВ, распределенной равномерно на отрезке 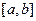 :
:
Решение.
Найдем математическое ожидание по формуле (5):
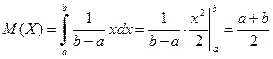 .
.
Найдем дисперсию по формуле (6):
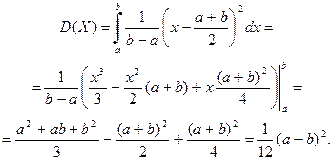
Можно найти дисперсию и другим способом:
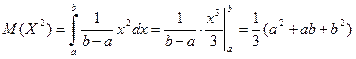 ,
,
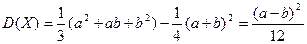 .
.
Отсюда, с учетом 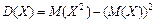 , получаем:
, получаем:
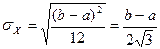 .
.
Нормальный закон распределения. Нормальным распределением (или распределением Гаусса) называется распределение НСВ, для которого плотность вероятности определяется формулой
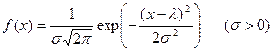 .
.
Для СВ, распределенной по нормальному закону:
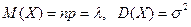 .
.
Вероятность попадания значений нормально распределенной СВ Х в интервал 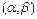 определяется формулой
определяется формулой
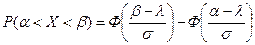 , (7)
, (7)
где Ф (х) – функция Лапласа:
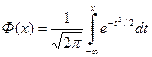 .
.
Значения функции Лапласа приведены в приложении. Для этой функции справедливо соотношение
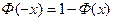 . (8)
. (8)
Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула:
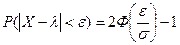 .
.
Пример.
Найти вероятность попадания в интервал (4, 9) значений нормально распределенной СВ Х, для которой математическое ожидание равно 8, а среднее квадратическое отклонение равно 1.
Решение.
Применим формулу (7), которая в данном случае примет вид:
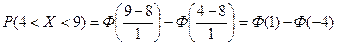 .
.
Используя далее соотношение (8), получаем окончательно:
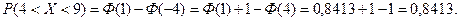
(Значения функции Лапласа Ф (х) найдены по таблице приложения.)
 2015-06-10
2015-06-10 451
451








