Равномерное распределение плотности вероятности

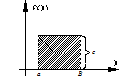
Данное распределение справедливо в том случае, если случайное событие лежит в определенном интервале времени от 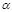до 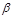и появление его в этом интервале равновероятно. Поскольку событие произойдет на интервале времени 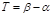отсюда вероятность его появления: 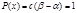, а 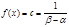. Функция распределения: 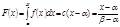. Математическое ожидание случайной величины будет определяться величиной: 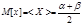, а дисперсия 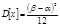. Дисперсия случайной величины при равномерном распределении растет пропорционально квадрату интервала. Это распределение равномерно.

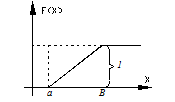Геометрическая интерпретация математического ожидания это координата центра тяжести плоской фигуры, ограниченной прямой плотности распределения и абсцисса. Дисперсия это момент инерции плоской фигуры относительно оси, проходящей параллельно оси плотности распределении через центр тяжести.