Нормальное (Гауссово) распределение плотности вероятности

Нормальное распределение используется в теории вероятности для описания событий, зависящих от многих факторов, каждый из которых слабо влияет на распределение случайных событий. По нормальному закону распределяются параметры серийной продукции, параметры износа. Плотность распределения: .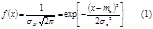

Распределение Гаусса зависит от двух параметров М(х) и Д(х). Кривая плотности симметрична относительно оси, параллельной оси ординат. Максимальное значение этой плотности равно 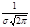. Вероятность попадания случайной величины распределенной по нормальному закону в заданный интервал 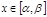: 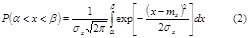. Для упрощения расчета используется табулированное выражение равенства (2), вводим новую переменную 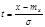, тогда 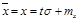, 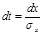. . 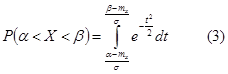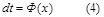- интеграл Лапласа или интеграл вероятности, тогда 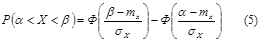. Интеграл вероятности обладает свойствами: Ф(0)=0, Ф( 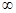)=0,5, Ф(-х)=-Ф(х).

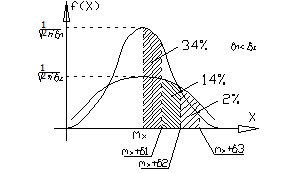
При нормальном распределении на интервале 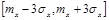срабатывает закон 3 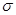, согласно которому в этом интервале попадание почти 100%, 97,7%, поэтому вероятность появления случайной величины вне этого интервала очень мала, менее 0,3%.