Операции над случайными событиями

Поскольку события являются подмножествами, то операции над ними такие же, как в теории множеств. Только в теории вероятностей употребляется терминология, несколько отличающаяся от теоретико-множественной.

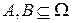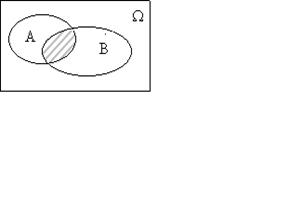
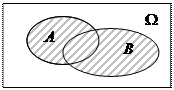
Суммой двух событий A и B, называется событие A + B 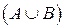,состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий A или B. Событие A + B наступает тогда и только тогда, когда наступает или событие A, или событие B.

Произведением двух событий A и B, 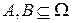называется событие AB 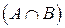, состоящее из элементарных событий, принадлежащих и A, и B. Событие AB наступает тогда и только тогда, когда события A и B наступают одновременно.

Операции суммы и произведения обобщаются по индукции на любое конечное или счетное число событий. Используемые при этом обозначения:

;

.

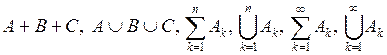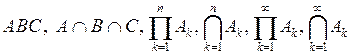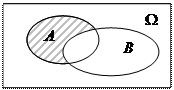Разностью двух событий A и B, 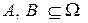называется событие 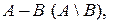состоящее из элементарных событий множества A, не принадлежащих B. Событие A-B происходит тогда и только тогда, когда происходит A, но не происходит B.

Событие W называется достоверным событием. Оно происходит всегда при проведении эксперимента.

Невозможным называется событие Æ, которое не может произойти при проведении эксперимента.

W

Событие 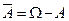называется противоположным событию A. Событие 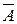происходит тогда и только тогда, когда А не происходит.

Говорят, что событие A влечёт событие B (или, что B следует из A), обозначается 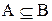, если все элементарные события, принадлежащие событию A, принадлежат также и событию B, то есть из наступления события A следует наступление события B.

Очевидно, что любое событие А влечет достоверное и следует из невозможного: .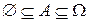

События A и B называются равносильными, обозначается A = B, если .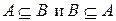

События A и B называются несовместными, если они не могут произойти одновременно: AB = Æ.

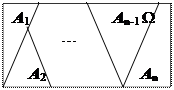
События 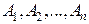образуют полную группу событий, если:

· они являются попарно несовместными: ;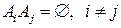

· в сумме дают событие достоверное: .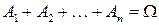

Пример.

Эксперимент состоит в подбрасывании игральной кости: .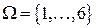

Рассмотрим события:

A = {Выпадение четного числа очков} = {2, 4, 6};

B = {Выпадение не более трех очков} = {1, 2, 3};

C = {Выпадение нечетного числа очков} = {1, 3, 5}.

Тогда 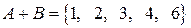, 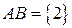; ; 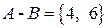; 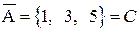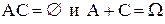, то есть А и С образуют полную группу событий.