Геометрическое определение вероятности является обобщением классического определения вероятности на случай, когда множество равновозможных исходов бесконечно.
Говорят, что случайный эксперимент удовлетворяет геометрическому определению вероятности, если:
· исходы эксперимента можно изобразить точками некоторой области 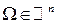 , имеющей конечную меру
, имеющей конечную меру 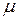 ;
;
· можно считать, что попадание точки в любые области 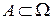 , имеющие одинаковую конечную меру
, имеющие одинаковую конечную меру 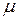 , равновозможно и не зависит от формы и расположения
, равновозможно и не зависит от формы и расположения 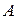 внутри
внутри 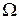 . При этом говорят, что точка равномерно распределена в области
. При этом говорят, что точка равномерно распределена в области 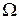 или бросается в область
или бросается в область 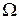 наудачу.
наудачу.
Согласно геометрическому определению вероятности вероятность попадания точки в любую область 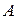 (событие
(событие 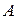 ) пропорциональна ее мере
) пропорциональна ее мере 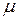 :
:
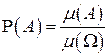 .
.
В частности:
при 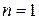 под мерой
под мерой 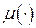 понимается длина
понимается длина 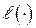 подмножества на числовой прямой
подмножества на числовой прямой  и
и
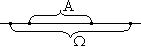
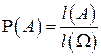 ;
;


|
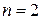 под мерой
под мерой 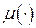 понимается площадь
понимается площадь 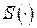 подмножества на плоскости
подмножества на плоскости 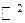 и
и
|
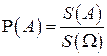 ;
;
 при
при 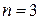 под мерой
под мерой 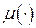 понимается объем
понимается объем 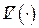 подмножества в пространстве
подмножества в пространстве 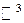 и
и

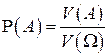 .
.
Замечание. В рассмотренной схеме событиями считаются не любые подмножества 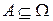 , а только имеющие конечную меру
, а только имеющие конечную меру 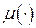 . Данное ограничение необходимо, поскольку в
. Данное ограничение необходимо, поскольку в 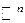 существуют неизмеримые (не имеющие меры) множества (см. замечание из раздела 1.2, а также раздел 1.7).
существуют неизмеримые (не имеющие меры) множества (см. замечание из раздела 1.2, а также раздел 1.7).
Из геометрического определения вероятности вытекают следующие свойства вероятности.
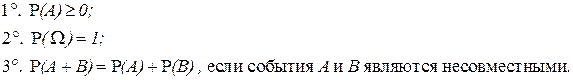
Следовательно, справедливы и свойства вероятности 4° – 7°, доказательство которых в классическом определении вероятности основывалось только на свойствах 1° – 3°.
Пример.
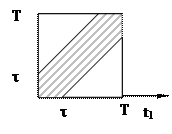
На обслуживающее устройство в промежутке времени 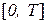 равновозможно поступление двух заявок. Время обслуживания одной заявки равно t. Если очередная заявка поступает в момент занятости устройства обслуживанием предыдущей, то она теряется. Найти вероятность потери заявки.
равновозможно поступление двух заявок. Время обслуживания одной заявки равно t. Если очередная заявка поступает в момент занятости устройства обслуживанием предыдущей, то она теряется. Найти вероятность потери заявки.
Решение. Обозначим t1, t2 - моменты поступления заявок. Тогда
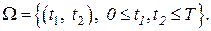 Интересующее нас событие А имеет вид:
Интересующее нас событие А имеет вид:
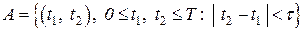 .
Поэтому (см. рисунок) .
Поэтому (см. рисунок)
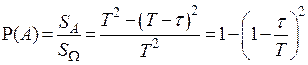 . .
|
|
 2015-06-10
2015-06-10 602
602