Свойства вероятности 1° – 3°, установленные в классическом, геометрическом и статистическом определениях вероятности, в аксиоматическом определении принимаются в качестве системы аксиом (только свойство 3° формулируется в более общем виде), а вероятность задается как функция (нормированная мера), определенная на множестве событий.
Прежде, чем переходить к аксиоматике, уточним понятие случайного события. Если пространство элементарных событий 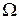 имеет конечное или счетное число элементов, то действительно в соответствии с определением из раздела 1.2 случайным событием можно считать любое подмножество
имеет конечное или счетное число элементов, то действительно в соответствии с определением из раздела 1.2 случайным событием можно считать любое подмножество 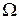 . Сложности возникают, когда пространство элементарных событий
. Сложности возникают, когда пространство элементарных событий 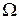 несчетно. Если и в этом случае под событием понимать любое подмножество
несчетно. Если и в этом случае под событием понимать любое подмножество 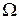 , то корректно определить его вероятность удается не всегда (см. замечание в разделе 1.5 и пример в конце данного раздела).
, то корректно определить его вероятность удается не всегда (см. замечание в разделе 1.5 и пример в конце данного раздела).
В связи с этим, класс подмножеств W, которые считают событиями, ограничивают. При этом естественно требуют, чтобы этот класс был замкнут относительно операций над событиями, т.е. чтобы результат выполнения операций над событиями (в том числе и в счетном количестве) был снова событием.
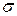 -алгебра событий
-алгебра событий
Определение. Пусть W - произвольное множество. Класс 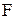 подмножеств множества W (не обязательно всех) называется
подмножеств множества W (не обязательно всех) называется 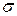 -алгеброй событий или
-алгеброй событий или
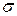 -алгеброй подмножеств W, если выполнены следующие свойства:
-алгеброй подмножеств W, если выполнены следующие свойства:
А1) 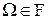 (
(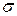 -алгебра событий содержит достоверное событие);
-алгебра событий содержит достоверное событие);
А2) если 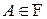 , то
, то 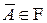 (вместе с любым событием
(вместе с любым событием 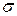 -алгебра содержит противоположное событие);
-алгебра содержит противоположное событие);
А3) если 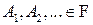 , то
, то 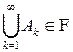 (вместе с любым конечным или счетным набором событий
(вместе с любым конечным или счетным набором событий 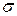 -алгебра содержит их сумму).
-алгебра содержит их сумму).
Свойства А1) – А3) часто называют аксиомами 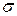 -алгебры.
-алгебры.
Проверим, что этого набора аксиом достаточно для замкнутости класса подмножеств 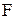 и относительно других операций над событиями.
и относительно других операций над событиями.
1. 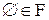 (
(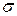 -алгебра событий содержит невозможное событие).
-алгебра событий содержит невозможное событие).
▲ Поскольку 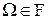 по А1), то
по А1), то 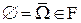 в силу А2). ■
в силу А2). ■
2. При выполнении А1) и А2) свойство А3) эквивалентно свойству А4):
А4) если 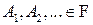 , то
, то 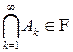 (вместе с любым конечным или счетным набором событий
(вместе с любым конечным или счетным набором событий 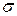 -алгебра содержит их произведение).
-алгебра содержит их произведение).
▲ Докажем, что при выполнении А1) и А2) из А3) следует А4).
Если 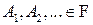 , то при всех
, то при всех 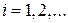 по свойству А2)
по свойству А2) 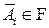 . Тогда из А3) следует, что
. Тогда из А3) следует, что 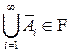 , и по А2) дополнение к этому множеству также принадлежит
, и по А2) дополнение к этому множеству также принадлежит 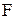 , то есть
, то есть 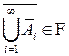 . Но в силу свойств двойственности
. Но в силу свойств двойственности 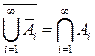 .
.
Доказательство в обратную сторону полностью аналогично. ■
3. Если 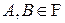 , то
, то 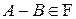 .
.
▲ 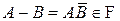 , так как
, так как 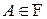 ,
, 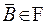 и по А4) их произведение также принадлежит
и по А4) их произведение также принадлежит 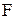 . ■
. ■
Множества 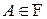 и только они далее будут считаться событиями, наступление которых возможно в результате данного случайного эксперимента.
и только они далее будут считаться событиями, наступление которых возможно в результате данного случайного эксперимента.
Пример. Пусть 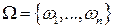 - конечное пространство элементарных событий. Следующие классы подмножеств
- конечное пространство элементарных событий. Следующие классы подмножеств  являются
являются 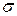 -алгебрами:
-алгебрами:
1. 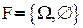 - тривиальная
- тривиальная 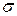 -алгебра.
-алгебра.
2. 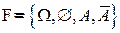 , где А – произвольное подмножество
, где А – произвольное подмножество 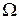 .
.
3. 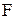 - множество всех подмножеств
- множество всех подмножеств 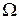 (доказать, что при этом число всех подмножеств в
(доказать, что при этом число всех подмножеств в 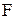 равно
равно 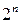 ).
).
Определим теперь вероятность как функцию, определенную на множестве событий (то есть функцию, которая каждому событию ставит в соответствие число), а точнее как неотрицательную нормированную меру, заданную на 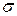 -алгебре событий
-алгебре событий 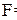 .
.
 2015-06-10
2015-06-10 1110
1110
