Схема независимых испытаний Бернулли

Предположим, что некоторый эксперимент может повторяться при неизменных условиях сколько угодно раз, и эти повторения не зависят друг от друга. В этом случае говорят о проведении последовательности независимых испытаний. Независимость испытаний при этом следует понимать в том смысле, что любые события, которые могут произойти в результате, являются независимыми в совокупности.

Простейшей является последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: успех – У (1) и неуспех – Н (0). Последовательность независимых испытаний с двумяисходами называется схемой независимых испытаний Бернулли.

Обозначим вероятность успеха 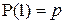, а вероятность неуспеха .

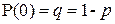При проведении n независимых испытаний по схеме Бернулли пространство элементарных событий имеет вид:

,

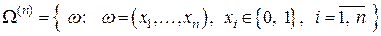а вероятности элементарных событий в силу независимости вычисляются по формуле:

,

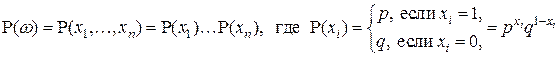то есть

.

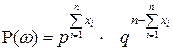В связи с рассмотрением схемы независимых испытаний Бернулли обычно представляют интерес события

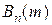={В n испытаниях наступило ровно m успехов} = = .

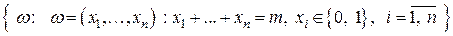Обозначим вероятность 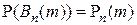и вычислим ее. Для любого 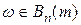вероятность 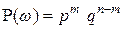, а общее количество исходов, содержащихся в 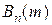, равно числу способов размещения m единиц в последовательности длины n из нулей и единиц, то есть 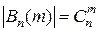. Таким образом,

.

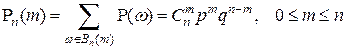Полученная формула называется формулой Бернулли. Она даёт выражение для вероятности наступления m успехов в n независимых испытаниях по схеме Бернулли с неизменной вероятностью успеха в одном испытании равной p и с вероятностью неуспеха равной q = 1 – p.

Поскольку события 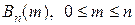образуют полную группу событий, то 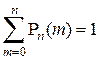. Тот же результат можно получить и на основании бинома Ньютона:

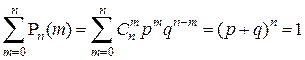
Исследуем поведение вероятностей 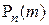в зависимости от m. Для этого вычислим отношение:

.

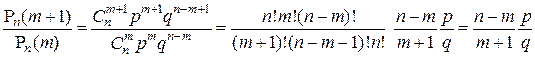Отсюда следует, что вероятности 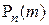возрастают, когда 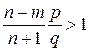или, что эквивалентно, .

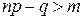Вероятности 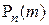убывают, когда 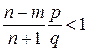или, что эквивалентно, .

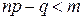И, наконец, 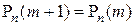, если .

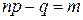Определение. Число успехов m = m₀, при котором вероятности 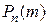достигают максимума, называются наивероятнейшим числом успехов.

Из проведённых рассуждений следует, что наивероятнейшее число успехов m₀ определяется из двойного неравенства:

.

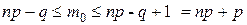При этом:

1. Если число 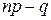нецелое, то существует одно наивероятнейшее число успехов: .

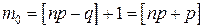2. Если число 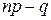целое, то существует два наивероятнейших числа успехов: 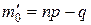и .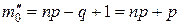

3. Если число 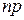целое, то .

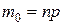Вычисления по формуле Бернулли при больших m и n весьма трудоёмкие. На практике в этом случае используют асимптотические приближения для вероятностей 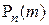, основанные на предельных теоремах Пуассона и Муавра-Лапласа.

Пример.

Что более вероятно: выиграть у равносильного противника 3 партии из 4 или 5 из 8 (ничьи не считаются)?

Решение.

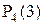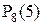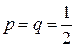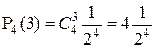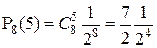В данном примере речь идет о сравнении двух вероятностей и , когда . Поскольку , а , то 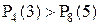, то есть выиграть 3 партии из 4 более вероятно.