2015-06-10
289
Нормальное распределение задается плотностью вероятности
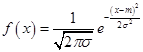
| (3.39) |
Можно показать, что функция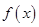 
удовлетворяет условию нормировки 
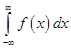= 1.
Кривая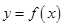 
имеет вид, изображенный на рис. 3.1.
 |
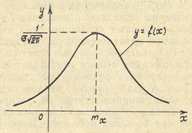Рис. 3.1.
Параметры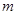 
и 
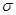в формуле (2.20) являются соответственно математическим ожиданием (
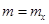) и средним квадратическим отклонением (
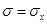) нормально распределенной случайной величины 
.
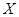Кривая нормального распределения 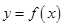симметрична относительно линии 
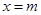, поэтому 
.
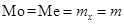Введем функцию Лапласа
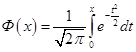
| (3.40) |
Таблица значений функции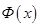 
приведена в прилож. 2. Свойства функции Лапласа
1) 
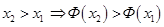, т.е. 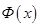монотонно возрастает.
2) 
;
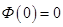3) 
;
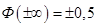4) 
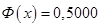, если 
;
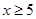5) 
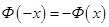, т.е. 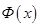нечетная функция.
Функция распределения для нормального закона находится через функцию Лапласа (2.21) по формуле
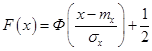
| (3.41) |
С помощью функции Лапласа находится вероятность попадания нормально распределенной случайной величины в заданный интервал:
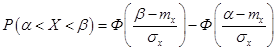
| (3.42) |
Для интервала, симметричного относительно математического ожидания, формула (2.23) дает следующее:
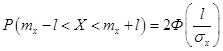
или
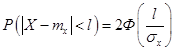
| (3.43) |
Если в формуле (2.24) положить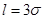 
, то получим
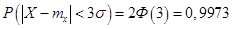
| (3.44) |
все (99,73%) значения нормально распределенной величины попадают в интервал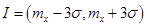 
. Этот факт называют «правилом трех сигм». Интервал I называется зоной практического рассеивания.
Нормальный закон встречается чаще всего в приложениях теории вероятностей. Им с большой моделируются реальные.распределения размеров и веса изделий в одной партии, отклонения точек попадания снаряда от цели, ошибки измерений, распределение людей по росту, по интеллектуальным возможностям и т. д.
